Punto materiale

• In Fisica, si definisce punto materiale un corpo privo di dimensioni, o le cui dimensioni sono trascurabili rispetto a quelle della regione di spazio in cui può muoversi e degli altri oggetti con cui può interagire.
• Esempio: se si vuole studiare il moto della Luna rispetto alla Terra, sia la Luna che la Terra possono essere approssimate a punti materiali, dato che le loro dimensioni sono molto più piccole rispetto alla loro distanza.

Velocità 1/2

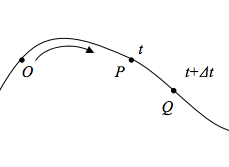
• Consideriamo un punto mobile P sopra una qualsiasi linea.
• Se P si muove sulla curva al variare del tempo t, allora \(\vec{s}\) sarà funzione di t e si scriverà: \( \quad\quad \vec{s} = \vec{s}(t)\)

• Se dopo un intervallo di tempo Δt, cioè all'istante t + Δt, il punto mobile si troverà in Q, lo spazio percorso a quell'istante sarà: \[\vec{s}(t + Δt) \]
• Osserviamo dunque che all'incremento Δt della variabile tempo corrisponde, per lo spazio, l'incremento: \[ \Delta \vec{s} = \vec{s}(t + \Delta t) - \vec{s}(t) \] che rappresenta lo spazio percorso da P nel tempo \(\Delta t\)

Velocità 2/2

• Si definisce velocità media del punto mobile: \[ \frac {\Delta \vec{s}}{\Delta t} = \frac{\vec{s}(t + \Delta t) - \vec{s}(t)}{\Delta t} \]
• Facciamo tendere a zero l'incremento Δt del tempo: \[ \lim_{\Delta t \to 0} \frac{\vec{s}(t + \Delta t) - \vec{s}(t)}{\Delta t} \]
• Si definisce velocità istantanea la derivata dello spazio rispetto al tempo: \[ \vec{v} = \lim_{\Delta t \to 0} \frac{\Delta \vec{s}} {\Delta t} = \frac{d\vec{s}}{dt} = \vec{s}^{'} \]

Accelerazione 1/2

• La velocità istantanea è una funzione del tempo t e quindi nell'intervallo \(\Delta t\) di tempo subirà la variazione: \[ \Delta \vec{v} = \vec{v}(v + \Delta t) - \vec{v}(t) \]
• Si definisce accelerazione media del punto materiale: \[ \frac {\Delta \vec{v}}{\Delta t} = \frac{\vec{v}(t + \Delta t) - \vec{v}(t)}{\Delta t} \]
• Si definisce accelerazione istantanea la derivata della velocità rispetto al tempo: \[ \vec{a} = \lim_{\Delta t \to 0} \frac{\Delta \vec{v}} {\Delta t} = \frac{d\vec{v}}{dt} = \vec{v}^{'} \]

Accelerazione 2/2

• L'accelerazione istantanea è la derivata della velocità rispetto al tempo e quindi è la derivata seconda dello spazio percorso rispetto al tempo.
\[ \vec{a}(t) = \frac{d \vec{v}(t)}{dt} = \frac{d}{dt} \frac{d \vec{s}}{dt} = \frac{d^2 \vec{s}(t)}{dt^2} = \vec{s}^{''}(t) \]

Moto rettilineo uniforme 1/2

• Un corpo si muove di moto rettilineo e uniforme se mantiene una velocità costante in modulo, direzione e verso.
• Legge oraria del moto rettilineo e uniforme: \[ \vec{v} = \frac{d\vec{s}}{dt} \Rightarrow d\vec{s} = \vec{v} dt \Rightarrow \int_{s_0}^s d\vec{s} = \int_{t_0}^t \vec{v} dt \] \[ t_0 = 0 \Rightarrow \vec{s} - \vec{s_0} = \vec{v} * t \Rightarrow \vec{s} = \vec{s_0} + \vec{v} * t \]

Moto rettilineo uniforme 2/2

Moto rettilineo uniformemente accelerato 1/2

• Un corpo si muove di moto rettilineo uniformemente accelerato se mantiene una accelerazione costante in modulo, direzione e verso.
• Legge oraria del moto rettilineo uniformemente accelerato: \[ \vec{a} = \frac{d\vec{v}}{dt} \Rightarrow d\vec{v} = \vec{a} \thinspace dt \Rightarrow \int_{v_0}^v d\vec{v} = \int_{0}^t \vec{a} \thinspace dt \Rightarrow \vec{v} = \vec{v_0} + \vec{a} \thinspace t \] \[ \frac{d\vec{s}}{dt} = \vec{v_0} + \vec{a} \thinspace t \Rightarrow d\vec{s} = \vec{v_0} dt + \vec{a} \thinspace t dt \Rightarrow \] \[ \int_{s_0}^{s} \vec{s} \thinspace ds = \int_0^{t} \vec{v_0} dt + \int_{0}^{t} \vec{a} \thinspace t dt \Rightarrow \vec{s} = \vec{s_0} + \vec{v_0} t + \frac{1}{2}\vec{a} t^2 \]

Moto rettilineo uniformemente accelerato 2/2

Moto parabolico

• Il moto parabolico è un tipo di moto bidimensionale esprimibile attraverso la combinazione di due moti rettilinei simultanei e indipendenti:
  • moto rettilineo uniforme
  • moto uniformemente accelerato.
• Si dimostra che la traiettoria del moto parabolico rappresenta una parabola.

Traiettoria del moto parabolico

• Si supponga che un corpo sia lanciato con velocità iniziale \(v_0\) e con un angolo \(\theta\) rispetto all'asse x orizzontale.
• Il vettore velocità può essere scomposto lungo le due componenti x e y: \[ \vec{v_0} = v_0 cos(\theta) \vec{i} + v_0 sen(\theta) \vec{j} \]
• Le leggi orarie dei moti lungo gli assi x e y sono: \[ x(t) = v_0 cos(\theta), \quad y(t) = v_0 sin(\theta) t - \frac{1}{2} g t^2 \]
• Esplicitando il parametro t dalla legge oraria x(t) e sostituendo in y(t) si ottiene una parabola con concavità rivolta verso il basso: \[ y = x * tang\theta - \frac{g}{2v_0^2cos^2(\theta)} * x^2 \]

Animazione del moto parabolico

Moto circolare

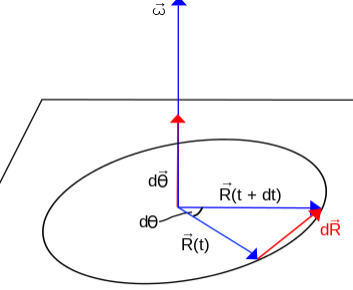
• Il moto circolare è il moto di un punto materiale lungo una circonferenza.
• Lo spostamento lineare del punto sulla circonferenza \(d\vec{R}\) sarà legato allo spostamento angolare \(d{\theta}\): \[ d\vec{R} = d\vec{\theta} \times \vec{R} \]

• La velocità angolare è definita come la derivata, rispetto al tempo, del vettore spostamento angolare: \[ \vec{\omega} = \frac{d\vec{\theta}}{dt} [\frac{rad}{s}] \Rightarrow \vec{v}(t) = \frac{d\vec{R}}{dt} = \vec{\omega} \times \vec{R} \]

Moto circolare uniforme

• Un corpo si muove di moto circolare uniforme se mantiene una velocità angolare costante in modulo, direzione e verso. \[ \vec{\omega} = \frac{d\vec{\theta}}{dt} = costante \Rightarrow d\vec{\theta} = \vec{\omega} * dt \] \[ \int_{\theta_0}^{\theta} d\vec{\theta} = \int_{o}^t \vec{\omega} * dt \Rightarrow \theta = \theta_0 + \omega * t \]

Moto circolare uniformemente accelerato

• Un corpo si muove di moto circolare uniformemente accelerato se mantiene un' accelerazione angolare in modulo, direzione e verso costante. \[ \vec{\alpha} = \frac{\vec{\omega}}{dt} = cost \]
• Integrando l'equazione differenziale \(\vec{\omega}(t) = \vec{\alpha} * dt\): \[ \omega(t) = \omega_0 + \alpha * t \] \[ \theta(t) = \theta_0 + \omega_0 * t + \frac{1}{2} \alpha * t^2 \]

Moto armonico - funzione periodica

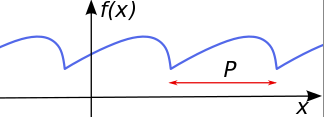
• In Matematica una funzione si dice periodica se assume valori che si ripetono esattamente a intervalli regolari.

• Le funzioni trigonometriche seno e coseno sono periodiche di periodo 2\(\pi\).

Moto Armonico 1/2

• Si definisce moto armonico il moto di un punto materiale la cui legge oraria è una funzione periodica del tipo: \[ x(t) = A sen(\omega t + \phi_0) \] dove A è l'ampiezza dell'oscillazione, \(\phi_0\) è la fase iniziale e \(\omega\) è la pulsazione
• Per un moto armonico così definito si dimostra che il periodo è: \[ T = \frac{2\pi}{\omega} \]

Moto Armonico 2/2

• La velocità e l'accelerazione sono rispettivamente la derivata prima e seconda della legge oraria, ovvero: \[ v(t) = \frac{d x(t)}{dt} = \omega A cos (\omega t + \phi); \] \[ d(t) = \frac{d v(t)}{dt} = -\omega^2 A sin (\omega t + \phi); \]

Rappresentazione grafica del moto armonico 1/2

Rappresentazione grafica del moto armonico 2/2