Risultati appello di Fisica I - 11-01-2014

Appello 11/01/2014 - Esercizio 1

• Un cilindro omogeneo di raggio r, altezza h e densità \(ρ_C\) galleggia su un liquido di densità \(ρ_L\) in posizione verticale lungo l'altezza h.
• Se gli viene impressa una leggera pressione, senza alcuna rotazione, si osserva che, una volta lasciato libero, compie un moto armonico.
• Determinare il periodo del moto.
• \((r = 10cm, ρ_C = 0.8g/cm3 , ρ_L = 1g/cm3 , h = 8cm)\)

Appello 11/01/2014 - Esercizio 1 - Soluzione

• In condizione di equilibrio, ovvero prima che al cilindro venga impressa una leggera pressione: \[ \vec R = 0 \Rightarrow P - S_{A} = 0 \Rightarrow \pi r^2 x_0 ρ_L g = m g \]
• Dopo che al cilidro viene impressa una leggera pressione: \[ \vec R = m \vec a \Rightarrow P - \pi r^2 (x_0 + x) ρ_L g = m \frac{d^2 x}{dt^2} \] \[ m \frac{d^2 x}{dt^2} + \pi r^2 ρ_L g * x = 0 \Rightarrow T = 2\pi \sqrt{\frac{ρ_C h }{ρ_L g }} \]

Appello 11/01/2014 - Esercizio 2

• Un cilindro avente sezione di 25 \(cm^2\) e contenente del gas ideale è chiuso da un pistone mobile, che ha massa 500 grammi e che si trova a un'altezza di 2 metri dal fondo del cilindro.
• Se l'energia interna del gas aumenta di 1 Joule in seguito a una trasformazione adiabatica, a che altezza si troverà il pistone rispetto al fondo del cilindro?

Appello 11/01/2014 - Esercizio 2 - Soluzione

• Una trasformazione adiabatica avviene senza scambi di calore quindi la variazione di energia interna è pari al lavoro subito o fatto.
• Per il primo principio della Termodinamica: \[ dU = -dW \Rightarrow \Delta U = 1 Joule \Rightarrow mg \Delta y = \Delta U \] \[ \Delta U > 0 \Rightarrow dW < 0 \Rightarrow \Delta y = - \frac{\Delta U}{mg} \] \[ y = h - \frac{\Delta U}{mg} = 180 cm \]

Appello 01/02/2014 - Esercizio 1

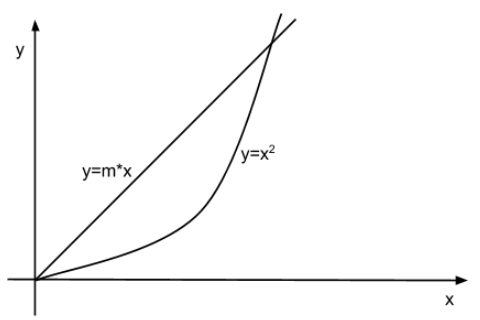
• Determina il momento d'inerzia rispetto all'asse x di un corpo avente densità di massa superficiale costante σ e la cui superficie è delimitata dalle curve \(y=mx\) e \(y=x^2\).

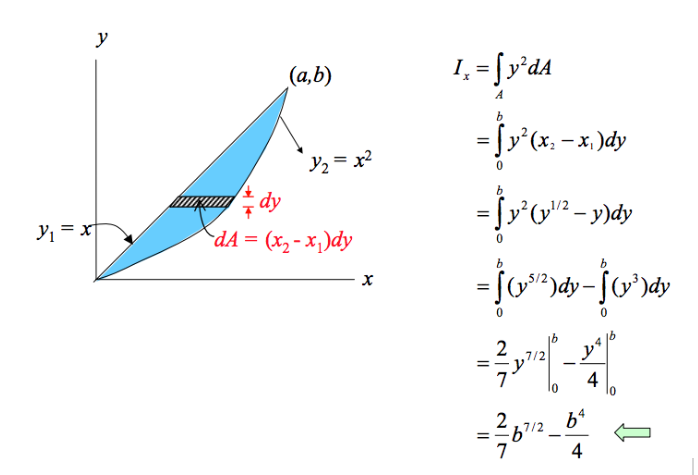
Appello 01/02/2014 - Esercizio 2 - soluzione

Appello 01/02/2014 - Esercizio 2

• Un recipiente avente il volume di 6 litri è diviso in due parti A e B separate da una parete mobile e conduttrice. Le pareti esterne sono adiabatiche. Lo scomparto A contiene una mole di gas monoatomico a temperatura \(T_A\) = 200K, mentre nello scomparto B c'è una mole di gas, anch'esso monoatomico, a temperatura \(T_B\) = 400K. La pressione è la stessa nei due scomparti.
• Calcolare la variazione dell'energia interna del sistema durante la trasformazione e pressione, temperatura e volume dei due scomparti A e B nello stato di equilibrio.

Appello 01/02/2014 - Esercizio 2 - Soluzione

• Lo stato finale di equilibrio prevede che nei due scomparti si abbia la stessa temperatura e la stessa pressione. Poiché il numero di moli è lo stesso, i due gas occuperanno lo stesso volume, pari a metà del volume complessivo
• Il gas B, più caldo, cede calore al gas A più freddo che, riscaldandosi si espande . A compie lavoro positivo e B fa lavoro negativo. Il Sistema non scambia energia con l’esterno, né tramite lavoro, né tramite calore, quindi l’Energia interna non varia ( ∆U=0)