Esercizio 1

Una massa m è sospesa, tramite una fune inestensibile di massa trascurabile e di lunghezza L, ad un punto fisso. L’angolo formato dal filo con la verticale è θ.
Determinare la velocità, in funzione dell’angolo θ, che deve essere impressa alla massa per farla muovere di moto circolare uniforme in un piano orizzontale.

Soluzione Esercizio 1 (1/2)

• Sono dati i seguenti dati: \[ m, L, \theta \]
• Dobbiamo trovare la velocità in funzione dell'angolo: \[ v_p(\theta) \]

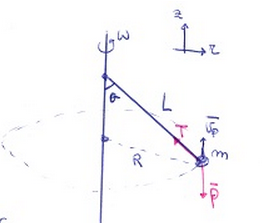
Soluzione Esercizio 1 (2/2)

• Scompongo le forze lungo i due assi z e r \begin{aligned} -T * \sin(\theta) = m * a_r \Rightarrow -T * \sin(\theta) = - m * \frac {v^2}{R} \end{aligned} \begin{aligned} -P + T\cos(\theta) = m * a_z \Rightarrow -P + T\cos(\theta) = 0 \end{aligned}
• Il modulo di \(\vec v\) è sempre uguale ma cambia di direzione e verso: \begin{aligned} v = \sin(\theta)*\sqrt\frac{L*g}{\cos(\theta)} \end{aligned}

Esercizio 3

Un corpo di massa m è posto sulla sommità di un piano inclinato a un'altezza h dal suolo, con il quale forma un angolo θ. Il piano è scabro con coefficiente di attrito statico pari a \(\mu_s\) e dinamico pari a \(\mu_d\).

• Calcolare il valore massimo dell'angolo di inclinazione \(\theta_m\) tale che per ogni θ minore di \(\theta_m\) la massa m resti in equilibrio.
• Calcolare il modulo dell’accelerazione \(\vec a\) del corpo ed il tempo \(t_f\) necessario per raggiungere il suolo.

Souluzione Ex 3 (1/2)

Souluzione Ex 3 (2/2)

Problem (Work, Energy) - Ex1

• A body slides down a rough plane inclined to the horizontal at \(30^0\).
• If 70% of the initial potential energy is dissipated during the descent, find the coefficient of sliding friction. (0.404)

Solution Ex1

• Potential energy: \( mgh = m * g * s * sin(\theta) .\)
• Friction: \(\mu * m * g cos (\theta) * s\)
• \(\mu * m * g cos (\theta) * s\ = \frac {70}{100} * m * g * s * sin(\theta) .\)
• \(\mu = 0.7\tan(\theta) = 0.7\tan(30^0) = 0.404\)

Problem (Work, Energy) - Ex2

• The potential energy of an object is given by \[ U(x) = 5x^2 - 4x^3 \] where U is in joules and x is in metres.
• What is the force, F(x), acting on the object?
• Determine the positions where the object is in equilibrium

Solution Ex 2

• For the force:
  \[F(x) = -\frac{dU}{dx} = -(10x -12x^2) = 12x - 10\]
• For equilibrium F(x) = 0 \[x(12x−10)=0 \Rightarrow x = \frac{5}{6} , x = 0\]

Problem (Work, Energy) - Ex 3

• A ramp in an amusement park is frictionless. A smooth object slides down the ramp and comes down through a height h.
• What distance d is necessary to stop the object on the flat track if the coefficient of friction is μ. (Solution: \(\mu = \frac{h}{d}\))

Solution - Ex 3

• At the bottom of the ramp the kinetic energy K available is equal to the loss of potential energy, mgh: \[K = m * g * h\]
• On the flat track the entire kinetic energy is used up in the work done against friction \[W = f_a * d = \mu * m * g * d = m * g *h\] \[\mu = \frac{h}{d}\]