Primo principio della Termodinamica
- Video introduzione
- Equilibrio termico
- Definizione di temperatura
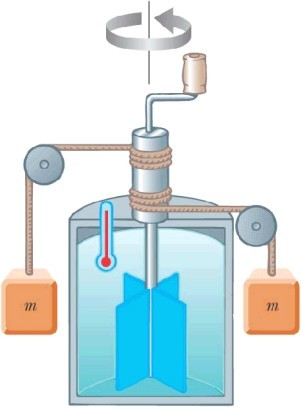
- Esperimento di Joule
- Primo principio della Termodinamica
- Trasmissione del calore
Antonio Pierro @antonio_pierro_
Per consigli, suggerimenti, eventuali errori o altro potete scrivere una email a antonio.pierro[at]gmail.com
Sistema termodinamico e ambiente
- Il sistema termodinamico è una porzione di spazio materiale che può essere costituita da una o più parti, per esempio il volume di un gas o un liquido in equilibrio con il suo vapore.
- L'ambiente è quell'insieme con cui il sistema termodinamico può interagire, per esempio un fluido in cui è immerso il sistema.
Sistema aperto/chiuso
- Se tra il sistema termodinamico e l'ambiente:
- avvengono scambi di energia e di materia, il sistema è detto aperto.
- avvengono solo scambi di energia, il sistema si dice chiuso.
- non avvengo scambi di energia e di materia, il sistema si dice isolato.
Variabili di stato
- Per i sistemi a molte particelle non è possibile dare posizione e velocità di ogni particella contemporaneamente.
- Si descrive il sistema mediante pochi parametri legati ai valori medi delle grandezze dinamiche:
- Volume (\(m^3\))
- Pressione (Pascal o Pa): dovuta agli urti delle particelle sulle pareti.
- Temperatura (Kelvin o K): legata al valore medio delle energie cinetiche delle particelle.
Equilibrio termodinamico
- L'equilibrio termodinamico è il risultato di tre tipi di equilibrio:
- equilibrio meccanico: inteso come equilibrio di forze e momenti, secondo quanto studiato in Meccanica.
- equilibrio chimico: quando non avvengono traformazioni chimiche.
- equilibrio termico: quando la temperatura è costante ovunque.
Equilibrio termico tra due sistemi
- Dati due sistemi termodinamici A e B, aventi rispettivamente temperatura \(T_A\) e \(T_B\), si dicono in equilibrio termico se hanno la stessa temperatura:
\[
T_A = T_B
\]
- Se il sistema A è in equilibrio termico con C e se il sistema B è in equilibrio termico con C, allora A è in equilibrio termico con B:
\[
T_A = T_C \text{ e } T_B = T_C \Rightarrow T_A = T_B
\]
Temperatura 3/3
- Sia X una grandezza fisica che varia con la temperatura (volume, lunghezza, pressione, ecc.).
- Il dispositivo che misura questa caratteristica X sarà chiamato termometro.
- Per definizione un termometro che misura il punto triplo dell'acqua dà il valore \(X_{pt}\):
\[
\theta(X_{pt}) = \alpha X_{pt} = 273 K
\]
- La temperatura T del sistema sarà quindi:
\[
T = 273 \frac{X}{X_{pt}} K
\]
Primo principio della Termodinamica 1/2
- Dati due stati A e B, la variazione di energia interna \(\Delta U = U(A) - U(B)\) è pari alla differenza del calore assorbito e dal lavoro compiuto.
\[
\Delta U = Q - W
\]
Questa relazione viene assunta come postulato basato sull'esperienza.
- Questa relazione contiene come caso particolare quello dell'esperimento di Joule.
Primo principio della Termodinamica 2/2
- Il termine energia interna U indica l'energia legata a proprietà interne al sistema, come moto molecolare o forze intermolecolari che dipendono dalla temperatura del sistema.
- Il primo principio della Termodinamica mette in evidenza l'esistenza di un meccanismo di scambio di energia che è riconducibile a fenomeni meccanici microscopici e a cui diamo il nome di calore.
- Joule trovò il seguente risultato: 1 Caloria = 4.186 Joule
Trasformazione ciclica o chiusa
- Se un sistema termodinamico esegue una qualsiasi trasformazione che lo riporti allo stato iniziale (trasformazione ciclica o chiusa) si ha:
\[
\Delta U = 0 \Rightarrow Q = W
\]
- Se nella trasformazione ciclica il sistema assorbe calore, esso fornisce lavoro (macchina termica):
\[
Q > 0 \text{ e } W > 0
\]
- Se il sistema cede calore, esso deve subire un lavoro:
\[
Q < 0 \text{ e } W < 0
\]
Trasformazioni infinitesime
- Per risolvere un problema specifico può essere utile considerare trasformazioni termodinamiche nelle quali le variabili cambiano di quantità infinitesime:
\[
dQ = dU - dW
\]
- Per una trasformazione finita, integrando, si ha:
\[
\Delta{U} = \int_A^B dU = U_B - U_A, \quad Q_{AB} = \int_A^B dQ
\]
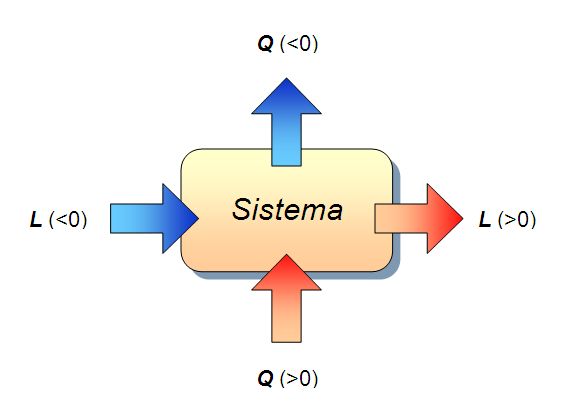
Convenzione sui segni 1/2
| Flusso di energia |
Segno |
| Calore che entra in un sistema dall'esterno |
Q > 0 |
| Lavoro che è compiuto da un sistema sull'esterno |
L > 0 |
| Calore che esce da un sistema verso l'esterno |
Q < 0 |
| Lavoro che è compiuto sul sistema dall'esterno |
L < 0 |
Convenzione sui segni 2/2
Trasformazione reversibile
- Una trasformazione si dice reversibile se in ogni punto i parametri di stato sono definiti.
- Una trasformazione reversibile può essere arrestata in qualunque stato intermedio e, variando di poco le condizioni esterne, si può invertire il verso della trasformazione.
Trasformazione irreversibile
- Una trasformazione si dice irreversibile quando i parametri di stato non sono definiti punto per punto.
- Una trasformazione irreversibile può avvenire in una sola direzione e, una volta raggiunto lo stato finale, non è possibile tornare allo stato iniziale.
- Sono presenti forze dissipative.
Trasformazione reversibile (esempio)
Trasformazione irreversibile (esempio)
- Un corpo con velocità iniziale \(\vec{v}\) viene frenato dall'attrito con il piano su cui si muove fino a fermarsi.
- L'energia cinetica diminuisce e contemporaneamente si osserva un aumento di temperatura delle superfici a contatto.
- Successivamente i corpi riscaldatisi cedono calore all'ambiente e alla fine la loro temperatura risulta essere pari alla temperatura ambiente.
- Complessivamente sparisce l'energia cinetica, ma viene ceduto calore all'ambiente in quantità uguale.
Propagazione del calore
- Il trasferimento del calore tra sistemi può avvenire nei seguenti modi:
- Conduzione
- Convezione
- Irraggiamento
Conduzione, legge di Fourier 1/2
- Il flusso di calore \(\frac{dQ}{dt}\)scambiato fra due pareti solide di confine a diversa temperatura può essere calcolato attraverso la legge di Fourier:
\[
d\Phi = \frac{dQ}{dt} = - k \thinspace \vec{\nabla} T \thinspace \thinspace \vec{dS} =
- k \thinspace dS \thinspace \vec{\nabla} T \thinspace \thinspace \vec{n}
\]
dove \(\vec{n}\) è il versore normale all'area infinitesima dS, T è la temperatura e K la costante di conducibilità termica.
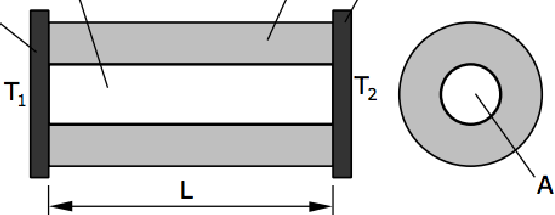
Conduzione, legge di Fourier 2/2
- direttamente proporzionale alla differenza di temperatura dT, all'area A della sezione trasversale e
- inversamente proporzionale alla lunghezza L:
\[
d\Phi_x = - k A \frac{dT}{dx} \Rightarrow \frac{\Phi_x}{A}\int_0^Ldx = - \int_{T_1}^{T_2}kdT \Rightarrow
\Phi_x = \frac{A k}{L} (T_1 - T_2)
\]
Convezione

Irraggiamento - legge di Stefan-Boltzmann
- Ogni corpo assorbe e irraggia onde elettromagnetiche, che si propagano anche nel vuoto, secondo la legge di Stefan-Boltzmann:
\[
\frac{dE}{dT} = \epsilon \sigma S T^4
\]
- dove \(\frac{dE}{dt}\) è l’energia dissipata per unità di tempo, \(\epsilon\) è l'emissività del
corpo, \(\sigma\) è la costante di Stefan ed S è l'area della superficie irraggiante.
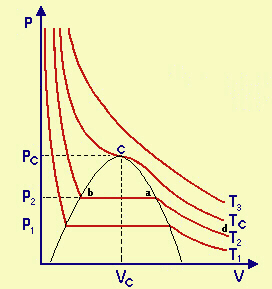
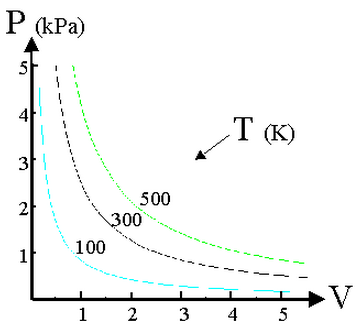
Diagramma P-V
- Ciascuna delle curve mette in relazione il volume e la pressione a
temperatura costante ed è detta isoterma.
Gas ideale
- È evidente che non esiste un gas perfetto nella realtà.
Legge dei gas perfetti o ideali
Le tre leggi empiriche della Chimica
La legge dei gas perfetti riassume le tre leggi empiriche della Chimica:
| Legge di Boyle |
\(V \propto \frac{1}{P}\) |
n e T costanti |
| Legge di Gay-Lussac |
\(V \propto T\) |
n e P costanti |
| Legge d'Avogadro |
\(V \propto n\) |
T e P costanti |
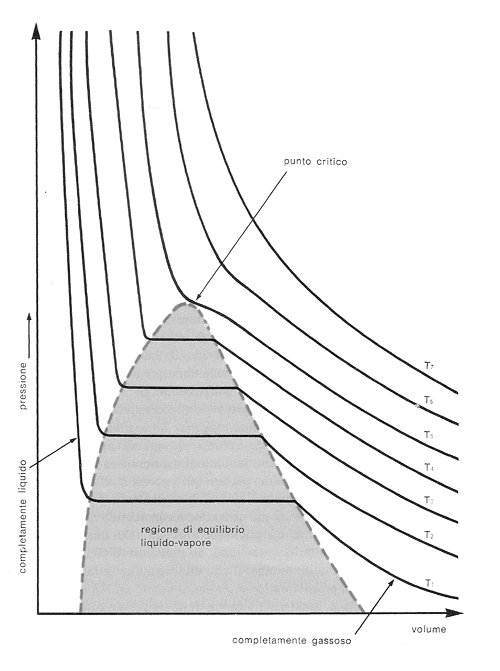
Equazione di van der Waals
Scambio di calore
- Il calore dQ, che si deve fornire o sottrarre per variare di una quantità dT la temperatura
di una sostanza di massa m, è pari a
\[
dQ = c * m * dT \Rightarrow Q = m \int_{T_A}^{T_B} c dT
\]
- Il calore specifico di una sostanza, c, è definito come la quantità di calore necessaria per aumentare (o diminuire) la temperatura di una unità di massa di 1 K (o equivalentemente di 1ºC).
- Il prodotto C = m * c è detto capacità termica del corpo.
Calore specifico
- Il calore specifico di una sostanza dipende dalla trasformazione fisica a cui tale sostanza è sottoposta, e in particolare dalla grandezza fisica x conservata nella trasformazione.
- Nel caso di un sistema gassoso si definiscono i calori specifici a volume o a pressione costante:
\[
c_v = \frac{1}{n}(\frac{dQ}{dT})_{V=costante}, \quad c_p = \frac{1}{n}(\frac{dQ}{dT})_{P=costante}
\]
e integrando:
\[
Q = n \int_{T_A}^{T_B} c_v dT, \quad Q = n \int_{T_A}^{T_B} c_p dT
\]
Calore specifico per un gas ideale
- In un gas ideale i calori specifici o sono costanti o dipendono soltanto dalla temperatura; vale per essi la relazione di Mayer:
\[
c_p - c_v = R
\]
-
Per i calori specifici dei gas ideali, si trovano sperimentalmente i seguenti risultati:
| gas monoatomici |
\(c_v = \frac{3}{2}R\) |
\(c_p = \frac{5}{2}R\) |
| gas biatomici |
\(c_v = \frac{5}{2}R\) |
\(c_p = \frac{7}{2}R\) |
Dimostrazione della relazione di Mayer 1/2
- Per il primo principio della Termodinamica:
\[
dQ = dU +dW \Rightarrow dQ = nC_V dT + P dV
\]
- Differenziamo l'equazione dei gas perfetti:
\[
PV = nRT \Rightarrow P * dV + V * dP = n * R * T
\]
- Sostituendo:
\[
nC_V dT + n * R * T - V * dP = dQ
\]
\[
\Rightarrow n(C_V + R)dT - V dP = dQ
\]
Dimostrazione della relazione di Mayer 2/2
- Si consideri una trasformazione isobara (pressione costante):
\[
n(C_V + R)dT = dQ
\]
- Si consideri il calore specifico a pressione costante:
\[
n * C_P = (\frac{dQ}{dT})_{P=cost}
\]
-
Avendo fatto una trasformazione isobara:
\[
n(C_V + R)dT = dQ \Rightarrow n(C_V + R) = \frac{dQ}{dt} = n * C_P
\]
\[
C_V + R = C_P \Rightarrow C_P - C_V = R
\]
Cambiamenti di fase
- Il cambiamento di fase è un processo isotermico in cui il sistema cambia fase (per esempio dalla fase solida alla fase liquida).
- Questi cambiamenti avvengono con scambio di calore tra sistema e ambiente, data dalla formula:
\[
Q = m \lambda
\]
-
m è la massa che cambia di fase e \(\lambda\) è il calore latente dello specifico cambiamento di fase, pari al calore che occorre cedere o sottrarre all'unità di massa della sostanza per farle cambiare di fase.
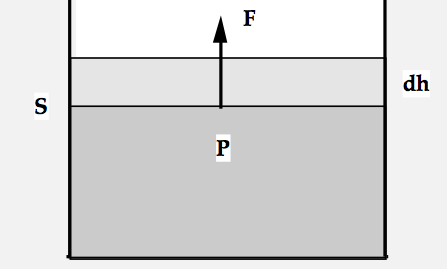
Il lavoro in Termodinamica 1/2
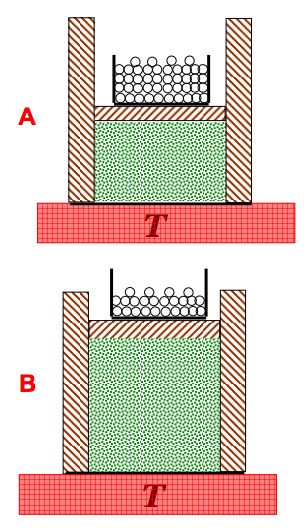
- Se P è la pressione esercitata dal gas sul pistone allora:
\[
dW = F * dh = P * S * dh; \quad dV = S * dh \Rightarrow dW = P * dV
\]
- Si noti che se il lavoro viene fatto dall'esterno (cioè spostando il pistone verso il basso), allora dV < 0 e quindi il lavoro dW è negativo.
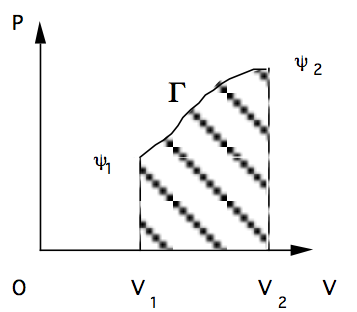
Il lavoro in Termodinamica 2/2
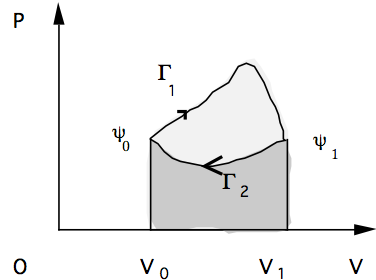
- Si noti che il lavoro compiuto durante la trasformazione \(\Gamma\) è dato dall'area della figura tratteggiata e che in generale dipende dalla trasformazione.
Il lavoro in una trasformazione ciclica
- Il lavoro compiuto dal sistema durante la trasformazione ciclica è dunque:
\[
W_{\Gamma} = \int_{\Gamma_1} P * dV + \int_{-\Gamma_2} P * dV = \int_{\Gamma_1} P * dV - \int_{\Gamma_2} P * dV
\]
che rappresenta l'area grigio chiaro del disegno.
Trasformazioni di un gas
| Trasformazione |
Grandezza costante |
| Isobara |
Pressione |
| Isocara |
Volume |
| Isoterma |
Temperatura |
| Adiabatica |
Calore |
Trasformazione isobara (gas ideale)
\[
P = \text{costante} \Rightarrow \frac{V_1}{V_2} = \frac{T_1}{T_2}
\]
Trasformazione isocora (gas ideale)
\[
V = \text{costante} \Rightarrow \frac{P_1}{P_2} = \frac{T_1}{T_2}
\]
Trasformazione isoterma (gas ideale)
\[
T = \text{costante} \Rightarrow P * V = \text{costante}
\]
Trasformazione adiabatica (gas ideale)
- Per il primo principio della Termodinamica:
\[
dU = dQ - dW, \quad dQ = 0 \Rightarrow dU = -dW \Rightarrow C_{V}dT = p dV
\]
- Si dimostra che per un gas ideale vale la seguente relazione:
\[
P * V^{\gamma} = \text{costante}, \quad \gamma = \frac{C_P}{C_V}
\]