Perpetuum mobile

• Nelle trasformazioni cicliche lo stato finale coincide con quello iniziale, dunque: \[ dU = 0 \Rightarrow dW = dQ \]
• Se ciò fosse vero, sarebbe possibile costruire una macchina che assorbendo calore lo trasforma completamente in lavoro meccanico.

• Una simile macchina potrebbe continuare a produrre lavoro indefinitamente ed è per questo che si chiama perpetuum mobile.

Considerazioni

• Si può affermare che il calore è una forma di energia a una scala gerarchica inferiore rispetto al lavoro.
• Esso rappresenta, in un certo senso, una forma degradata di energia, perchè non tutto il calore può essere ritrasformato in lavoro, mentre è vero il contrario.

Il ciclo di Carnot 1/4

• Col ciclo di Carnot si dimostra come sia possibile trasformare in lavoro il calore assorbito da due sorgenti termiche a differenti temperature \(T_1\) e \(T_2\) (\(T_1> T_2\)).
• Viene usato come ciclo di riferimento per applicazioni reali come, ad esempio, pompe di calore e frigoriferi.

Il ciclo di Carnot 2/4

Il ciclo di Carnot 3/4

1. Espansione isotermica (1-2) alla temperatura \(T_1\).
   È un'espansione con dU = 0 quindi: \[ dU = dq - dW \Rightarrow W_{12} = Q_{12} > 0 \]
2. Espansione adiabatica (2-3) dQ = 0. È ancora un'espansione (dW>0) quindi: \[ dU = dq - dW \Rightarrow U_3 - U_2 = -W_{23} < 0 \]

Il ciclo di Carnot 4/4

3. Compressione isotermica (3-4) alla temperatura \(T_2\).
   È una compressione (dW < 0) con dU = 0 , cioè: \[ dU = dq - dW \Rightarrow W_{34} = Q_{34} < 0 \]
4. Compressione adiabatica (4-1) dQ = 0. È una compressione (dW < 0) e quindi: \[ dU = dq - dW \Rightarrow U_{1} - U_{4} = -W_{14} > 0 \] cioè l'energia interna aumenta portando il sistema dalla tempertura \(T_1\) alla temperatura \(T_2\)

Rendimento di un ciclo di Carnot

• Il rendimento di una macchina termica è, in generale, il rapporto tra il lavoro utile che la macchina riesce a compiere e il calore totale assorbito dal sistema: \[ \eta = \frac{W}{Q_{assorbito}} \]
• Per il ciclo di Carnot: \[ \eta = \frac{Q_1 - Q_2}{Q_1} = 1- \frac{Q_2}{Q_1} = 1 - \frac{T_2}{T_1}, \quad \text{(T in Kelvin)} \]
• Si vede subito che il rendimento è massimo solo per \(T_2 = 0K\) (temperatura irraggiungibile per qualsiasi corpo)

Dimostrazione del rendimento

• Il lavoro totale lungo un ciclo completo: \[ W = W_{12} + W_{23} + W_{34} + W_{41} = R T_1 ln(\frac{V_2}{V_1}) - R T_2 ln(\frac{V_3}{V4}) \]
• Per una trasformazione adiabatica vale \(P V ^{\gamma} = K\) \[ \begin{cases} P_2 V_2^{\gamma} = P_3 V_3^{\gamma} = k_1 \\ P_4 V_4^{\gamma} = P_1 V_1^{\gamma} = k_2 \end{cases} \]
• Per la legge dei gas perfetti (\(P V = n R T\)): \[ \frac{P_2 V_2 V_2^{\gamma-1}}{P_1 V_1 V_1^{\gamma-1}} = \frac{K_2}{K_1} \Rightarrow \frac{V_2}{V_1} = \sqrt[1 - \gamma]{\frac{K_2}{K_1}} =\frac{V_3}{V_4}\]

1° teorema di Clausius 1/3

• Consideriamo il ciclo di Carnot di un gas perfetto: \[ dQ = dW \Rightarrow W_{12} = \int_{1}^{2} \frac{nRT}{V}dV \Rightarrow Q_{1} = RT_{1}ln(\frac{V_2}{V_1}) \]
• Analogamente, per la seconda isoterma: \[ Q_{2} = - RT_{2}ln(\frac{V_3}{V_4}) \]
• Avendo già dimostrato che in un ciclo di Carnot: \[ \frac{V_2}{V_1} = \frac{V_3}{V_4} \Rightarrow \frac{Q_1}{T_1} - \frac{Q_2}{T_2} = 0 \]

1° teorema di Clausius 2/3

• In generale per una qualsiasi trasformazione reversibile, se poniamo un sistema S a contatto con n sorgenti alle temperature \(T_1, T_2, .. T_n\), si ha: \[ \sum_{i=1}^n \frac{Q_i}{T_i} = 0 \] dove \(Q_i\) è da intendersi positivo se il calore è assorbito dal sistema e negativo nel caso opposto.
• Si può anche dimostrare che l'equazione precedente per cicli irreversibili diventa: \[ \sum_{i=1}^n \frac{Q_i}{T_i} < 0 \]

1° teorema di Clausius 3/3

• Se lo scambio di calore avviene con una serie infinita di sorgenti, detto dQ il calore scambiato con la sorgente a temperatura T: \[ \oint \frac{dQ}{T} \leq 0 \] dove l'integrale è da intendersi calcolato lungo una qualsiasi trasformazione ciclica e l'uguaglianza è vera solo per cicli reversibili.

L'entropia 1/3

• Il 1° teorema di Clausius permette di definire una nuova funzione di stato, l'entropia, per i sistemi termodinamici il cui significato più profondo è connesso con la probabilità che lo stato stesso si manifesti.
• Vogliamo ora definire l'entropia mediante la quantità di calore scambiato e la temperatura alla quale avviene lo scambio.

L'entropia 2/3

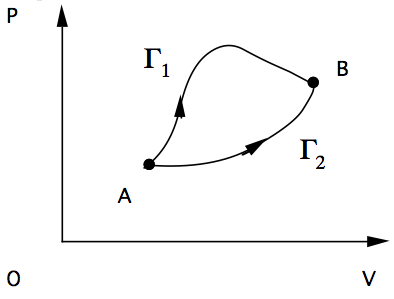
• Consideriamo due trasformazioni reversibili \(\Gamma_1\) e \(\Gamma_2\) mediante le quali il sistema passa dallo stato iniziale A allo stato finale B.
• Applicando il 1° teorema di Clausius al ciclo \(\Gamma = \Gamma_1 - \Gamma_2\) otteniamo:

L'entropia 3/3

• Poichè tale proprietà è vera per qualsiasi trasformazione reversibile, possiamo definire una funzione S che dipende solo dallo stato iniziale e quello finale: \[ dS = (\frac{dQ}{T})_{reversibile} \]

Calcolo dell'entropia per un gas ideale

• Utilizzando il primo principio della Termodinamica e la definizione di lavoro: \[ dU = dQ - dW \Rightarrow dQ = nC_V dT + PdV \]
• Utilizzando l'equazione dei gas ideali: \[ \int\frac{dQ}{T} = n C_V \int\frac{dT}{T} + \int\frac{pdV}{T} = n C_V \int\frac{dT}{T} + \int\frac{n R dV}{V} \] \[ \int\frac{dQ}{T} = n C_V ln(T) + n R ln(V) + S_0 = n ln(T^{C_V} * V^{R}) + S_0 \]