Circonferenza

• Definiamo circonferenza il luogo geometrico dei punti del piano equidistanti da un punto fisso detto centro

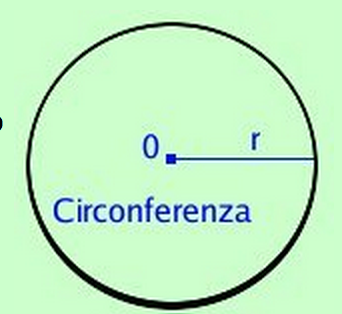
Cerchio

• Definiamo cerchio la parte finita di piano delimitata da una circonferenza

Definizioni sulla circonferenza

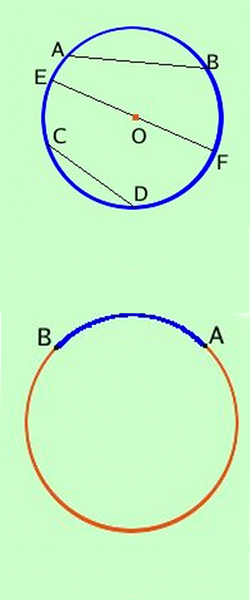
• La CORDA è il segmento congiungente due punti sulla circonferenza. AB, CD, EF sono corde.
• Il DIAMETRO è una corda che passa per il centro O della circonferenza EF è anche diametro oltre che corda
• La SEMICIRCONFERENZA è una delle due parti in cui la circonferenza viene divisa da un diametro
• L'ARCO è la parte di circonferenza compresa fra due suoi punti;

Definizioni sul cerchio

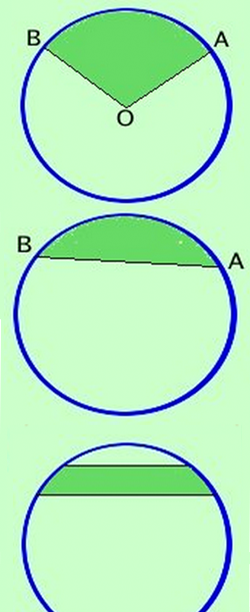
• Il SETTORE CIRCOLARE è la parte di cerchio compresa fra due raggi e la relativa parte di circonferenza
• Il SEGMENTO CIRCOLARE AD UNA BASE è la parte di cerchio compresa fra una sua corda e la circonferenza
• Il SEGMENTO CIRCOLARE A DUE BASI è la parte di cerchio compresa fra la circonferenza e due sue corde parallele
• La CORONA CIRCOLARE è l'insieme di punti del piano compresi tra due cerchi concentrici.

Relazione fra archi e corde

• In ogni circonferenza gli archi e gli angoli al centro che tali archi sottendono sono tra loro in proporzionalità diretta.
• In particolare significa:
  • Se gli archi sono congruenti allora sono congruenti anche gli angoli al centro e viceversa esempio.
  • Se un arco è doppio, triplo... di un altro anche l'angolo al centro corrispondente è doppio, triplo, ... dell'angolo al centro corrispondente

Mutue posizioni fra due circonferenze 1/2

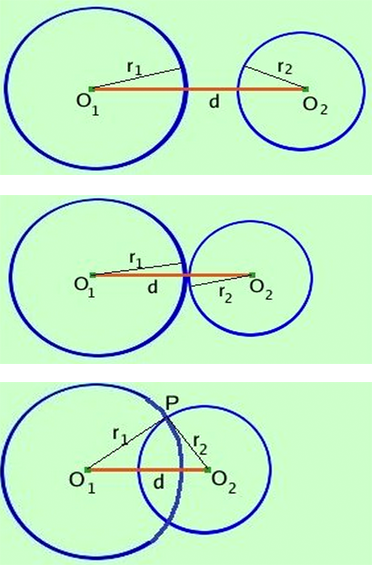
• Le circonferenze sono fra loro esterne se la distanza d fra i due centri è superiore al valore della somma dei due raggi \[ d=\overline{O_1 O_2} > r_2 + r_1 \]
• Le circonferenze sono fra loro tangenti esternamente se la distanza d fra i due centri è uguale al valore della somma dei due raggi
• Le circonferenze sono fra loro secanti se la distanza d fra i due centri è inferiore al valore della somma dei due raggi e superiore alla loro differenza

Mutue posizioni fra due circonferenze 2/2

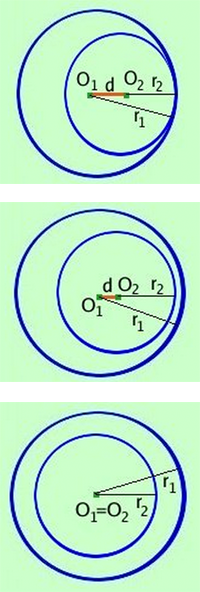
• Le circonferenze sono fra loro tangenti internamente se la distanza d fra i due centri è uguale al valore della differenza dei due raggi
• Una circonferenza è interna rispetto all'altra se la distanza d fra i due centri è inferiore al valore della differenza dei due raggi ma è maggiore di zero
• Le circonferenze sono concentriche se la distanza d fra i due centri è uguale a zero.

Angoli al centro ed alla circonferenza

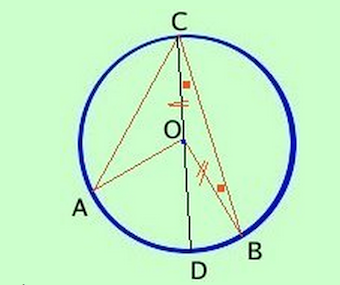
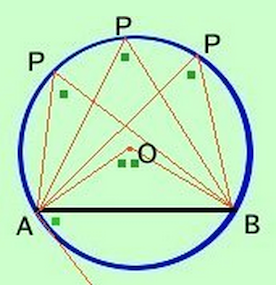
• Teorema: In ogni circonferenza l'angolo al centro è doppio dell'angolo alla circonferenza che insiste sullo stesso arco.
• Conseguenza immediata del teorema è che tutti gli angoli alla circonferenza che insistono sullo stesso arco sono congruenti (infatti sono tutti congruenti alla meta' dello stesso angolo al centro)

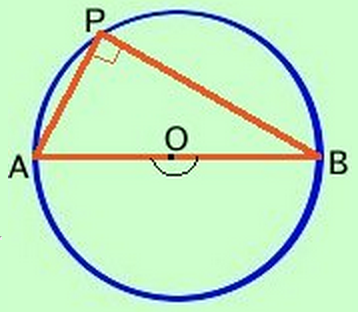
Triangolo rettangolo inscritto in una semicirconferenza

• Ogni triangolo inscritto in una semicirconferenza è rettangolo
• Dimostrazione: l'angolo \(A\hat{P}B\) è metà dell'angolo piatto \(A\hat{O}B\)
• Vale anche il viceversa

Circonferenza e punti notevoli del triangolo

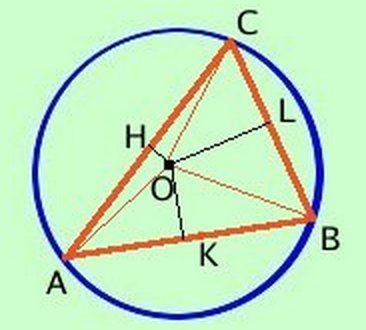
• Il circocentro (punto di incontro degli assi dei suoi lati) è il centro della circonferenza circoscritta al triangolo.
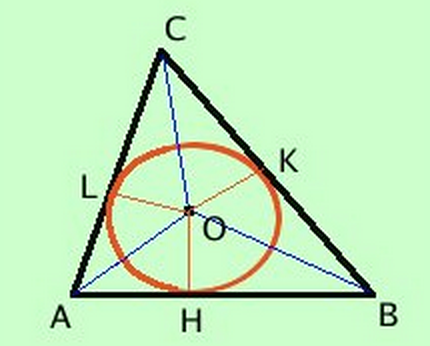
• L'incentro (punto di incontro delle bisettrici dei suoi angoli) è il centro della circonferenza inscritta nel triangolo.

Pi greco

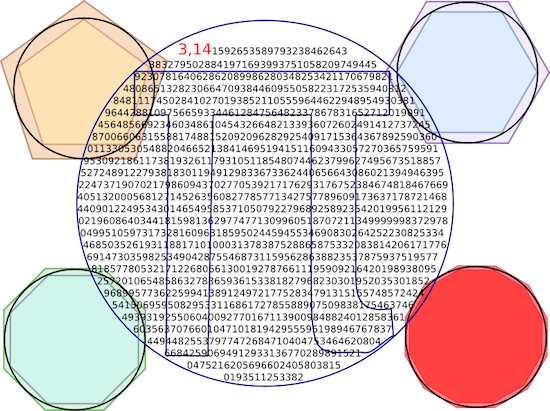
• Il Pi greco è una costante matematica indicata con la lettera greca \(\pi\).
• Nella geometria piana, \(\pi\) viene definito come il rapporto tra la misura della lunghezza della circonferenza e la misura della lunghezza del diametro di un cerchio.
• Le prime tre cifre decimali di \(\pi\) sono: 3,141...

Alcune formule che riguardano \(\pi\)

• Il perimetro di un cerchio di raggio r:     \(C = 2 * \pi * r \)
• L'area di un cerchio di raggio r: \[A = \pi * r^2\]
• Il volume di una sfera di raggio r: \[V = \frac{4}{3} * \pi * r^3\]
• La superficie di una sfera di raggio r: \[S = 4 * \pi * r^2\]