Relazioni fra rette nello spazio 1/2

• Due rette nello spazio possono essere:
  • Complanari: cioè giacciono su uno stesso piano
  • Sghembe: cioè non giacciono sullo stesso piano
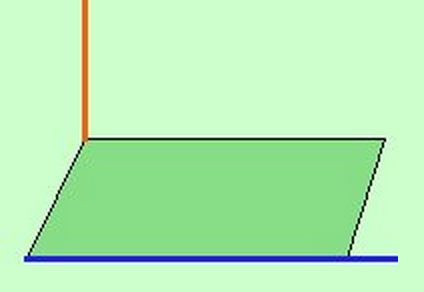
• In figura la retta rossa e la retta blu sono tra loro sghembe.

Relazioni fra rette nello spazio 2/2

• Una retta nello spazio rispetto ad un piano può essere:
  • Secante: in tal caso ha un solo punto in comune con il piano
  • Parallela ad una retta del piano: in tal caso non ha nessun punto in comune con il piano
  • Giacente sul piano: in tal caso ha tutti i punti in comune con il piano.
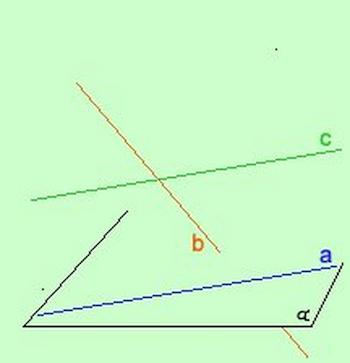
• Nella figura: la retta "a" giace sul piano, la retta "b" è secante il piano, la retta "c" è sopra il piano e parallela alla retta "a"

Angoloidi

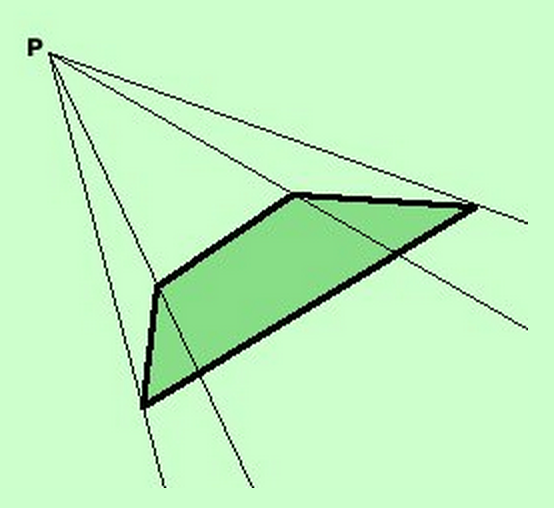
• Consideriamo un poligono ed un punto esterno al piano su cui giace il poligono:
• Definiremo angoloide lo spazio limitato da tutte le semirette uscenti dal punto dato e passanti per i punti del poligono (perimetro del poligono)
• Il punto P è chiamato vertice dell'angoloide.

Triedri

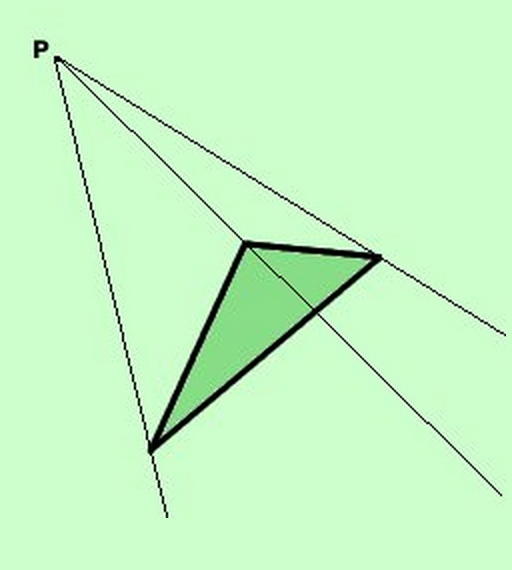
• Se il poligono "generatore" è un triangolo otteniamo l'angoloide più semplice che chiameremo Triedro
• Il triedro è lo spazio limitato da tutte le semirette uscenti dal punto dato, non giacente sul piano di un triangolo, e passanti per i punti dei lati del triangolo
• Il punto P è chiamato vertice del triedro

Poliedro

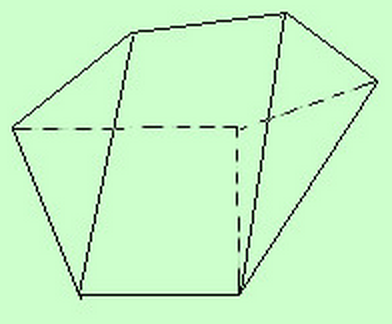
• Il poliedro è la parte di spazio limitata da un numero finito di poligoni, giacenti su piani diversi ed aventi, due a due, un lato in comune
• Ogni poligono si chiama Faccia
• L'insieme delle facce si chiama Superficie poliedrica

• La parte di spazio limitata dalla superficie poliedrica si chiama Volume del poliedro
• I lati dei poligoni si chiamano spigoli del poliedro
• I vertici dei poligoni si chiamano vertici del poliedro

Tipo di poliedro

• Il tipo di poliedro è individuato dal numero di facce della superficie poliedrica:
  • Tetraedro: poliedro con 4 facce
  • Pentaedro: poliedro con 5 facce (esempio: piramide)
  • Esaedro: poliedro con 6 facce (esempio: cubo)

Prisma indefinito

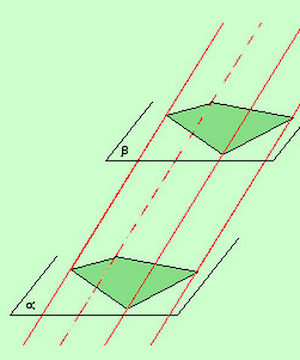
• Consideriamo un poligono qualunque sul piano \(\alpha\) e consideriamo un poligono congruente ad esso sul un altro piano \(\beta\) parallelo ad \(\alpha\)
• Consideriamo poi le congiungenti i punti corrispondenti dei perimetri dei due poligoni congruenti: in tal modo l'insieme di tali rette definiscono una "superficie prismatica" indefinita.
• La parte di spazio circondata dalla superficie prismatica è chiamata "prisma indefinito"

Prisma 1/2

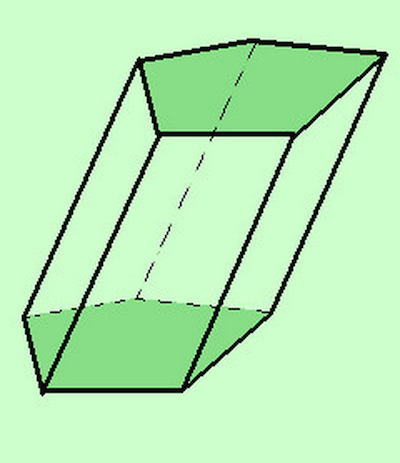
• Si dice prisma la parte di spazio racchiusa da un prisma indefinito compresa fra due sezioni parallele.
• Le sezioni parallele sono chiamate basi del prisma.
• Le altre facce diverse dalle basi sono chiamate facce laterali (sono sempre parallelogrammi).
• Se gli spigoli laterali sono perpendicolari alle basi avremo un prisma retto; il prisma in figura, invece, è obliquo.

Prisma 2/2

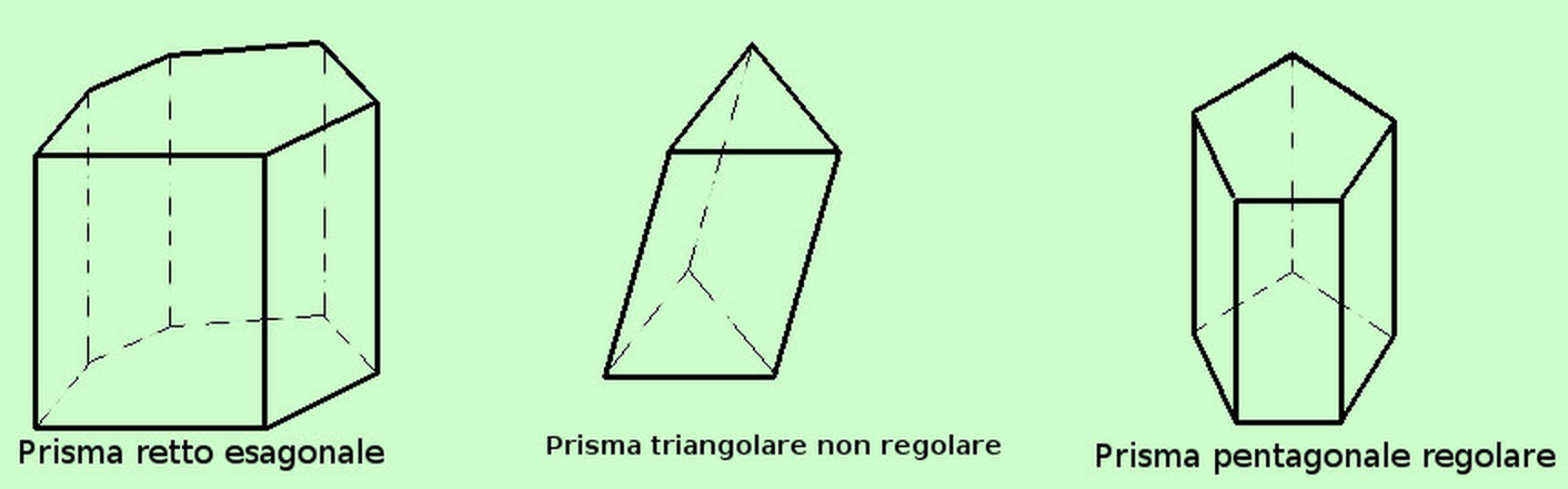
• Se i poligoni di base del prisma retto sono poligoni regolari diremo che il prisma è regolare

Concetto di volume

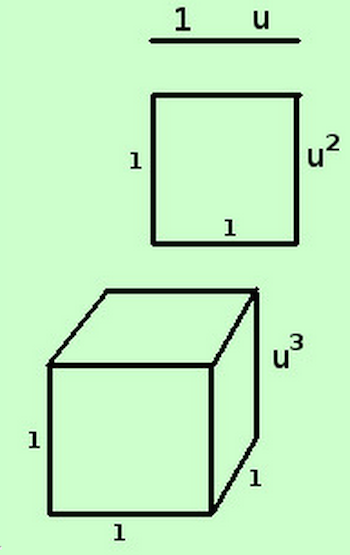
• Il volume è inteso come spazio racchiuso entro la superficie di un solido.
• Siccome per misurare dobbiamo usare una unità che sia dello stesso tipo dell'oggetto misurato useremo uno dei solidi più semplici: il cubo.
• Come unità di misura nello spazio useremo il cubo unitario, cioè il cubo con lato l'unità di misura lineare.

Volume del parallelepipedo rettangolo

• Il volume del parallelepipedo rettangolo si misura con il prodotto delle sue tre dimensioni: \[ V = a * b * h \]
• Il cubo che può essere visto come un parallelepipedo rettangolo con le tre dimensioni uguali: \[ V = l * l * l = l^3 \]

Volume del parallelepipedo retto

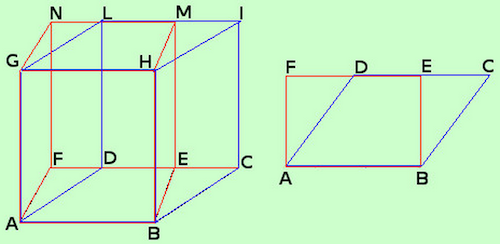
• Consideriamo il parallelepipedo retto (ABCDGHIL) (figura in blu) esso ha come base un parallelogramma.
• In rosso il rettangolo equivalente che diventa la base di un parallelepipedo rettangolo (ABEFGHMN)

• Il volume del parallelepipedo retto si trova moltiplicando l'area di base per la misura dell'altezza: \[ Volume = A_{superficie\ di\ base} * h \]

Volume del prisma retto

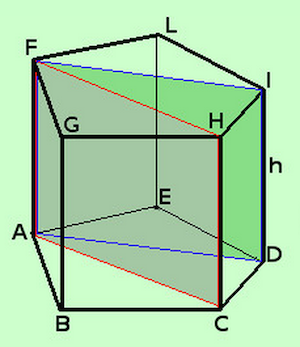
• Considerando un qualunque prisma retto (la base sarà un poligono con n lati)
• Il volume del prisma retto si trova moltiplicando l'area del poligono di base per la misura dell'altezza \[ Volume = A_{superficie\ di\ base} * h \]

Piramide

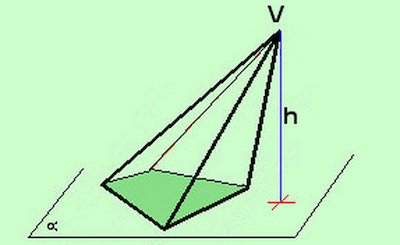
• Si definisce piramide la parte di spazio racchiusa da un angoloide ed un piano non passante per il vertice dell'angoloide e che ne intersechi tutti gli spigoli.
• Chiameremo:
  • il poligono base della piramide
  • i triangoli dell'angoloide facce laterali
  • la distanza fra il punto V ed il piano altezza h della piramide

Piramide retta

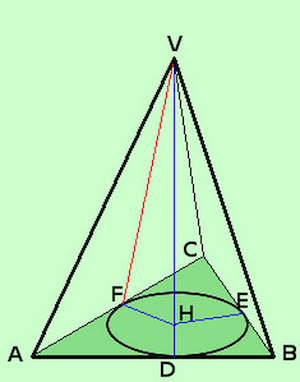
• Consideriamo l'insieme dei poligoni circoscritti ad una circonferenza
• se la nostra piramide ha come base uno di tali poligoni e la perpendicolare dal vertice cade esattamente nel centro del cerchio inscritto nel poligono allora diremo che tale piramide è retta
• Diremo infine regolare una piramide retta che abbia come base un poligono regolare

Area della superficie della piramide retta

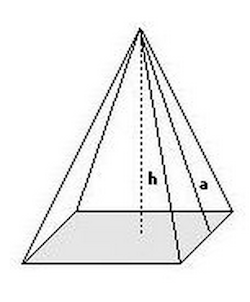
• Se la piramide è retta, le altezze di tutte le facce sono congruenti e si chiamano apotema.
• L'area della superficie laterale di una piramide retta si ottiene moltiplicando la lunghezza del perimetro di base per quella dell'apotema e dividendo il prodotto per 2. \[ A_{laterale} = \frac {p * a}{2} \]

• Se all'area della superficie laterale si aggiunge l'area della figura di base si ottiene l'area della superficie totale. \[ A_{totale} = A_{laterale} + A_{base} \]

Volume della piramide retta

• Poichè una piramide è equivalente alla treza parte di un prisma avente la base equivalente a quella della piramide e per altezza la stessa altezza il volume della piramide è un terzo di quello del prisma suddetto.
• Il volume di una piramide si ottiene moltiplicando l'area di base per la lunghezza dell'altezza e dividendo il prodotto per 3. \[ V = \frac{A_{base} * h}{3} \]

Definizione di cilindro

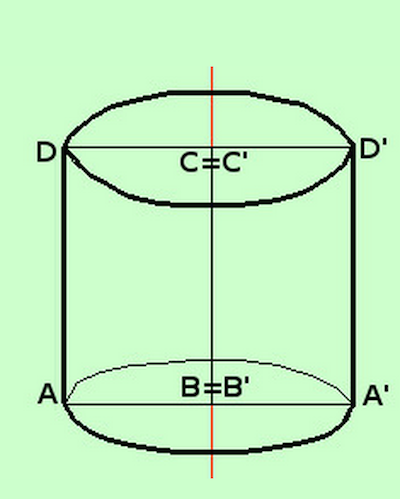
• Definiamo cilindro la parte di spazio percorsa da un rettangolo quando compie una rotazione completa attorno ad un suo lato
• AB = CD è il raggio del cilindro
• BC e' l'altezza del cilindro

Area della superficie del cilindro

• Sviluppando la superficie del cilindro su un piano otteniamo 2 cerchi (le basi) ed un rettangolo che è la superficie laterale.
• Essendo la base un cerchio il perimetro di base corrisponde alla lunghezza della circonferenza, quindi supponendo di conoscere il raggio di base r avremo che il perimetro di base vale: \(2 * \pi * r\)
• Se poi vogliamo calcolare l'area della superficie totale Ast dovremo sommare alla superficie laterale le aree delle due basi che corrispondono al doppio dell'area di un cerchio: \[ A_{superficie\ totale} = A_{sl} + 2 A_{sb} = 2 \pi r h + 2 \pi r^2 = 2 \pi r(h + r) \]

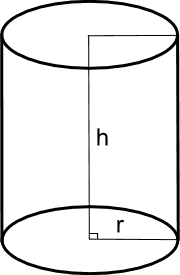
Volume del cilindro

• Il volume di un cilindro si ottiene moltiplicando l'area di base per la lunghezza dell'altezza: \[ V = \pi r^2 h \]

Definizione di cono

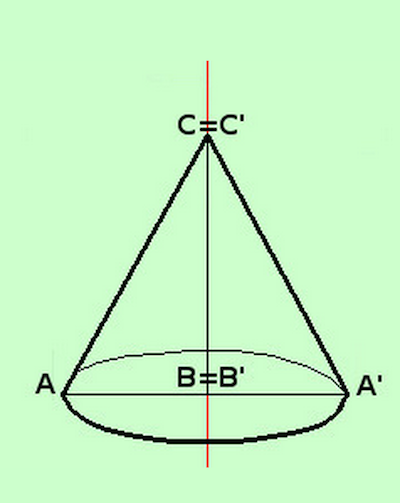
• Definiamo cono la parte di spazio percorsa da un triangolo rettangolo quando compie una rotazione completa attorno ad un suo cateto
• AB è il raggio = r del cono
• BC è l'altezza = h del cono
• AC è l'apotema = a del cono

Area della superficie del cono

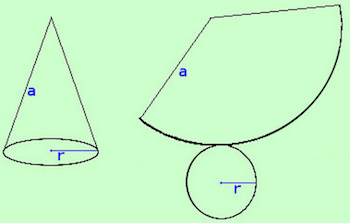
• Sviluppando la superficie del cono su un piano otteniamo la figura a destra.
• L'area del settore circolare si ottiene moltiplicando l'arco di base per l'apotema e dividendo il risultato per due. \[ A_{sl} = 2 \frac{\pi r a}{2} = \pi r a \]

• l'area della superficie totale \(A_{st}\) è la somma della superficie laterale e l'area di base che corrisponde all'area del cerchio: \[ A_{superficie\ totale} = A_{sl} + A_{sb} = \pi r a + \pi r^2 = \pi r (a + r) \]

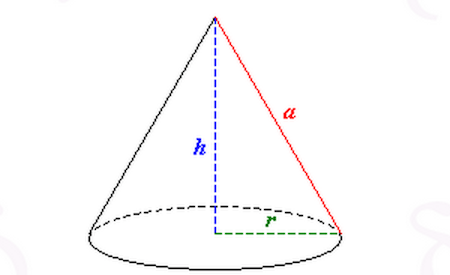
Volume del cono

• Il volume di un cono si ottiene moltiplicando l’area di base per la misura dell'altezza e dividendo tale prodotto per tre:: \[ V = \frac{A_{sb} * h}{3} = \frac{\pi r^2 h}{3} \]

Sfera

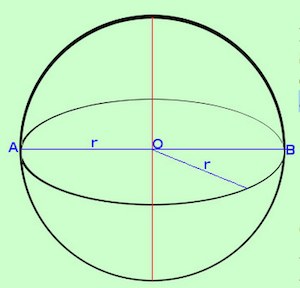
• Si definisce superficie sferica la zona dei punti dello spazio equidistanti da un punto fisso detto centro
• Si definisce sfera lo spazio limitato da una superficie sferica.

• Possiamo anche definire la sfera come solido di rotazione: area spazzata da una semicirconferenza in una rotazione completa attorno ad un suo diametro

Area e volume della sfera

• L'area della superficie di una sfera equivale a 4 volte l'area del suo cerchio massimo: \[ A_{sfera} = 4 \pi r^2 \]
• Il volume della sfera: \[ V = \frac{4}{3} \pi r^3 \]