Definizione di Poligono.

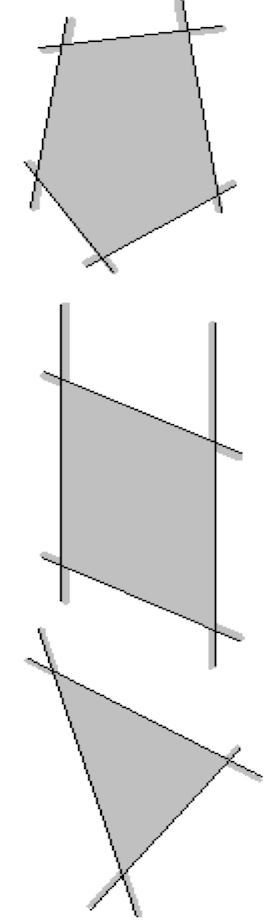
• Una figura piana è detta poligono quando è intersezione di semipiani.
• Tra i punti di intersezione delle rette che delimitano tali semipiani, quelli che appartengono al poligono si dicono VERTICI del poligono.
• I segmenti di tali rette che congiungono due vertici si dicono lati del poligono.

Lati/vertici consecutivi

• In un poligono, si dicono lati consecutivi due lati che hanno un vertice in comune
• In un poligono, si dicono vertici consecutivi due estremi di uno stesso lato

Perimetro

• Si chiama perimetro di un poligono la somma delle lunghezze dei suoi lati.

Diagonale

• Si dice DIAGONALE di un poligono, ogni SEGMENTO che UNISCE DUE dei suoi VERTICI NON CONSECUTIVI.

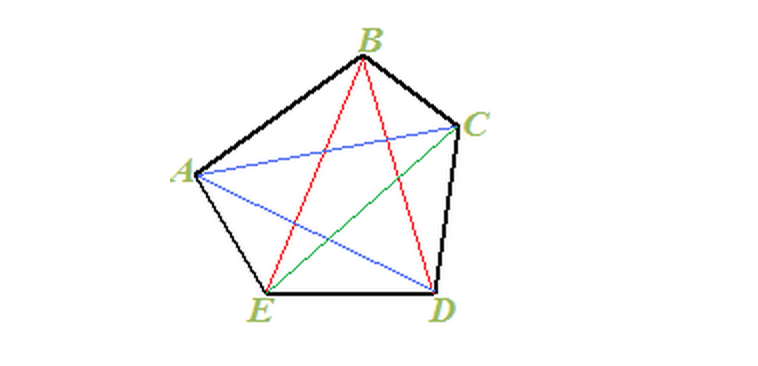
Teorema 1

• Un poligono con n lati ha \(\frac{n(n-3)}{2}\) diagonali
• La somma degli angoli di un poligono misura 180(n-2) gradi

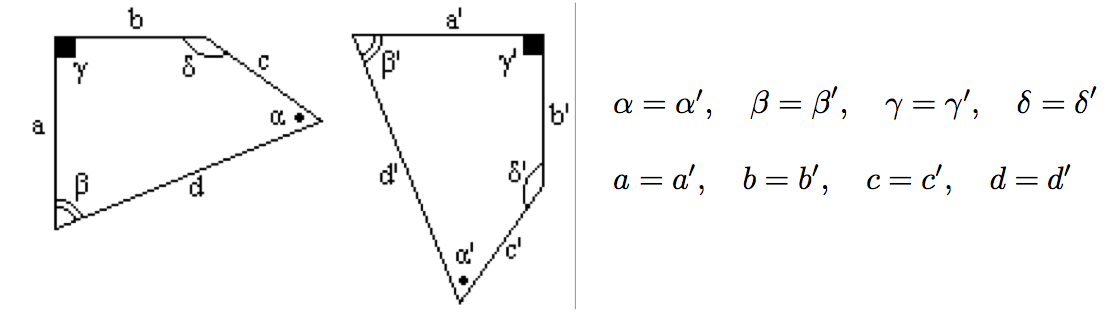
Teorema 2 - criterio di congruenza

• Due poligoni sono congruenti se e solo se hanno angoli e lati ordinatamente congruenti

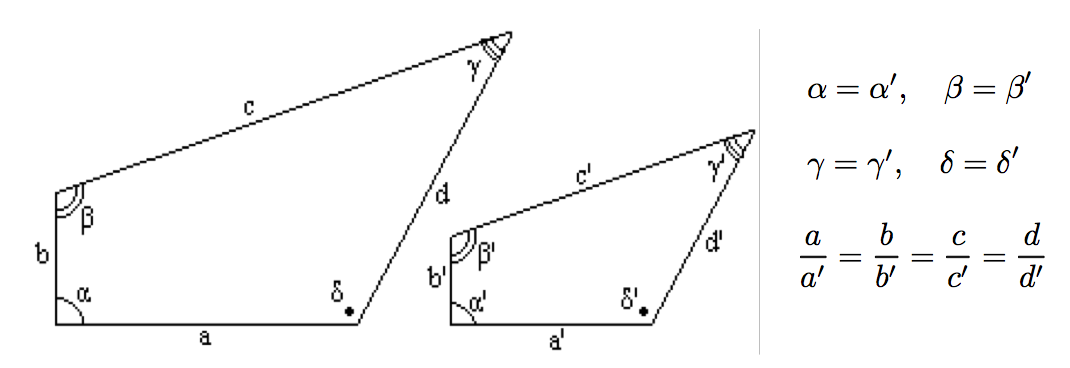
Definizione - Poligoni simili

• Due poligoni sono simili quando hanno (ordinatamente) angoli congruenti e lati proporzionali.

Definizione - Poligoni regolari

• Un poligono si dice regolare quando ha lati ed angoli tutti congruenti tra loro.
• Tutti i poligoni regolari con lo stesso numero di lati sono simili.
• Due poligoni regolari con lo stesso numero di lati sono congruenti se e solo se hanno la stessa area

AREA dei POLIGONI

• Per misurare l'estensione della superficie di un poligono dobbiamo confrontare tale superficie con un'altra superficie scelta come UNITA' DI MISURA in modo da stabilire quante volte quest'ultima è contenuta nella prima.
• Il numero di volte che l'UNITA' DI MISURA è contenuta nella superficie data si dice MISURA o AREA della superficie considerata.
• L'unità di misura delle superfici è il METRO QUADRATO, il cui simbolo è m2, con i suoi multipli e sottomultipli.

Area del rettangolo 1/2

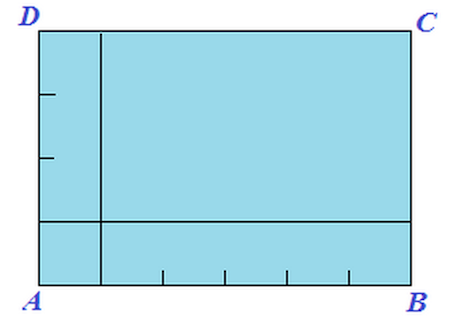
• Disegniamo il RETTANGOLO ABCD la cui base AB misura 6 m e e la cui altezza AD misura 4m
• Ora DIVIDIAMO la BASE e l'ALTEZZA del rettangolo in PARTI UGUALI, ciascuna di un metro di lunghezza
• Iniziamo a tracciare le rette parallele ai lati, passanti per i punti di divisione appena individuati

Area del rettangolo 2/2

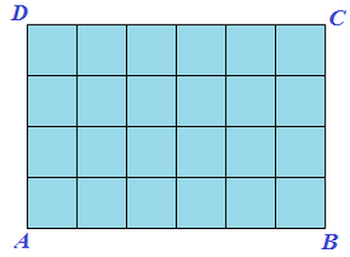
• Il rettangolo risulta diviso in 24 quadratini, ognuno dei quali ha il lato di un metro.
• Se ciascuno di questi quadratini ha il lato di 1 m, la sua superficie misura 1 m^2
• L'AREA del nostro rettangolo misura 24 m^2.
• Quindi possiamo affermare che l'AREA del RETTANGOLO è uguale al PRODOTTO della BASE per l'ALTEZZA.

AREA del PARALLELOGRAMMA

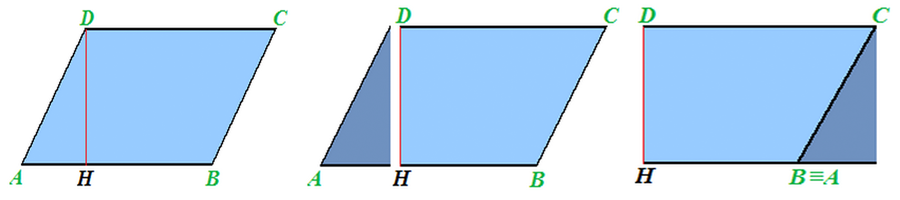
• Consideriamo il PARALLELOGRAMMA ABCD
• Tracciamo l'altezza DH rispetto alla base AB
• Ritagliamo il triangolo DHA e posizioniamo in modo diverso il triangolo appena ritagliato
• Per calcolare l'area del parallelogramma è sufficiente trovare l'area del rettangolo ad esso equivalente.

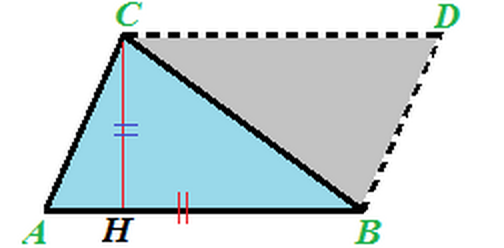
AREA del TRIANGOLO 1/2

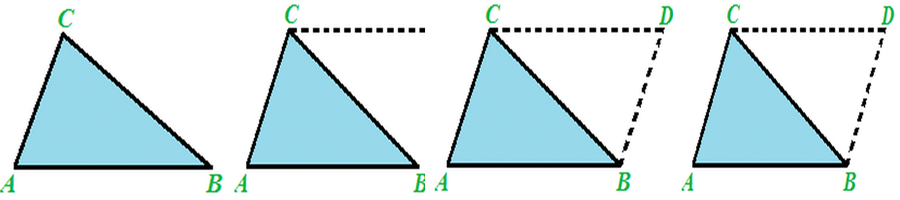
• Considero un qualsiasi TRIANGOLO ABC
• Partendo dal vertice C traccio la parallela al lato AB
• Partendo dal vertice B traccio la parallela al lato AC
• Sia la lettera D il punto di intersezione tra le due rette disegnate
• La figura che abbiamo ottenuto è quella di un PARALLELOGRAMMA

AREA del TRIANGOLO 2/2

• Un TRIANGOLO è EQUIVALENTE alla METÀ di un PARALLELOGRAMMA che ha la STESSA BASE e la STESSA ALTEZZA.
• L'AREA del TRIANGOLO si ottiene MOLTIPLICANDO la misura della BASE per quella dell'ALTEZZA ad essa relativa e DIVIDENDO il prodotto ottenuto PER DUE.
• La formula, quindi, è la seguente: A = (b x h)/2

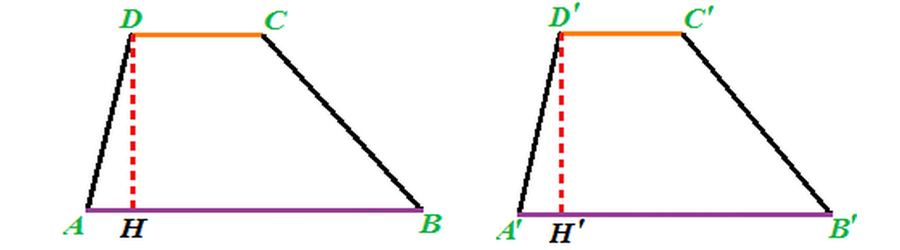
AREA del TRAPEZIO 1/3

• Disegniamo un TRAPEZIO ABCD
• Disegniamo un trapezio ad esso congruente che chiamiamo A'B'C'D'

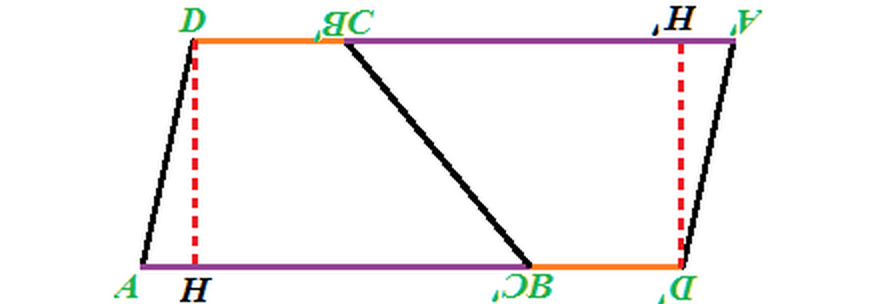
AREA del TRAPEZIO 2/3

• Ritagliamo i due trapezi e li posizioniamo uno accanto all'altro nel modo seguente
• Abbiamo ottenuto un PARALLELOGRAMMA.
• Il nostro PARALLELOGRAMMA quindi ha per altezza la STESSA ALTEZZA del trapezio e per base la SOMMA delle BASI del trapezio.

AREA del TRAPEZIO 3/3

• Un TRAPEZIO è EQUIVALENTE alla META' di un PARALLELOGRAMMA che ha per altezza la STESSA ALTEZZA del trapezio e per base la SOMMA DELLE BASI del trapezio.
• Quindi, l'AREA del TRAPEZIO si ottiene MOLTIPLICANDO la SOMMA delle misure delle BASI per la misura dell'ALTEZZA e DIVIDENDO il prodotto ottenuto per 2.