Punti, rette e piani
- Punti, rette e piani
- Segmenti
- Semiretta
- Semipiano
- Postulati di Euclide
Antonio Pierro @antonio_pierro_
Per consigli, suggerimenti, eventuali errori o altro potete scrivere una email a antonio.pierro[at]gmail.com
Punti, rette e piani 1/2
- Gli enti che assumiamo come primitivi, e mediante i quali definiremo gli altri oggetti geometrici sono i punti, le rette e i piani.
- Si usa indicare:
- i punti con lettere maiuscole: A, B, C, ... ;
- le rette con lettere minuscole: a, b, c, ... ;
- i piani con lettere minuscole greche: \(\alpha\), \(\beta\), \(\gamma\) ... .
Punti, rette e piani 2/2
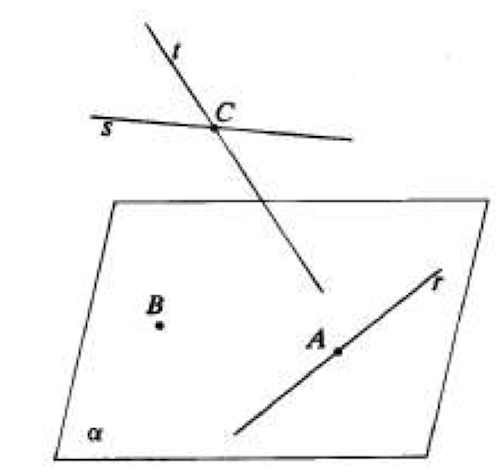
- il punto A appartiene alla retta r;
- la retta r passa per il punto A;
- i punti A e B appartengono al piano \(\alpha\)
- la retta r giace sul piano \(\alpha\)
- le rette s e t si intersecano nel punto C.
Segmento
- Data una retta r, fissiamo su di essa due punti A e B.
- Si chiama segmento AB il sottoinsieme della retta r costituito da tutti i punti P compresi fra A e B.
- I punti A e B si chiamano estremi del segmento AB.
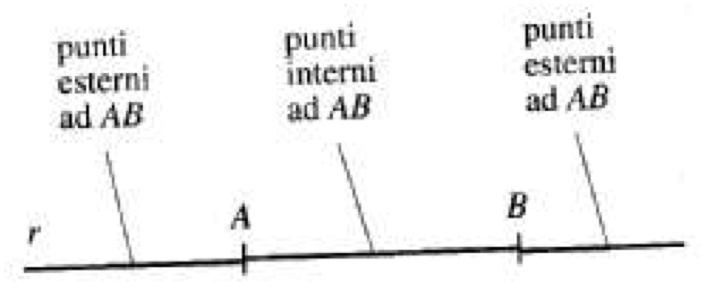
Segmenti consecutivi
- Si dice che due segmenti AB e BC sono consecutivi se hanno in comune soltanto un estremo, che, nel nostro caso, è B
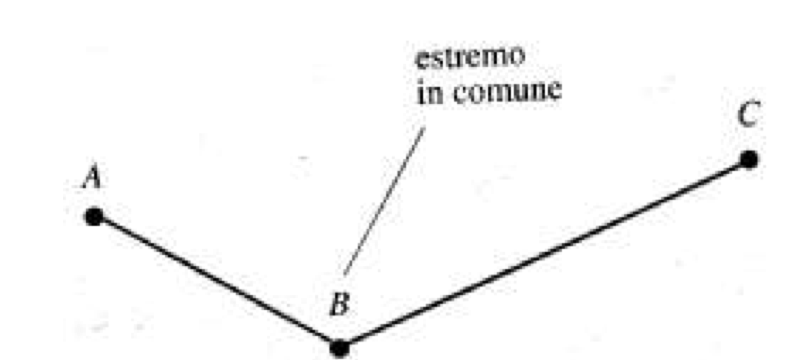
Segmenti adiacenti
- Si dice che due segmenti LM e MN sono adiacenti se sono consecutivi e appartengono alla stessa retta
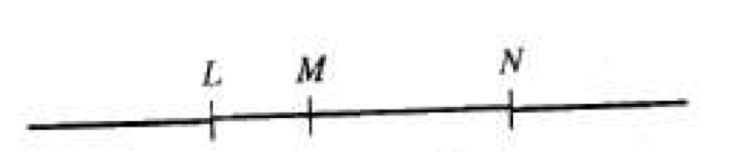
Semiretta
- Diciamo semiretta ciascuna delle due parti in cui una retta è divisa da un suo punto, a sua volta detto origine delle due semirette.
- Nella figura, il punto O divide la retta r nelle due semirette OA e OB.
- La semiretta è infinita, ha un inizio ma non una fine, e ha una sola dimensione: la lunghezza.

Semipiano
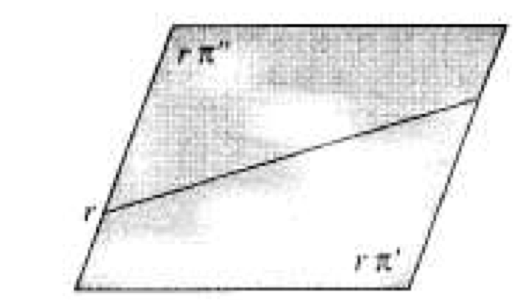
- Diciamo semipiano ciascuna delle due parti in cui un piano risulta diviso da una retta che giace sul piano stesso.
- La retta è detta origine dei due semipiani.
Rette parallele
- Due rette r ed s contenute nello stesso piano si dicono parallele se non hanno alcun punto in comune
- con linguaggio insiemistico: \(r \bigcap s = \varnothing \)
- Per indicare che r ed s sono parallele si scrive: \(r \parallel s\)

Rette incidenti
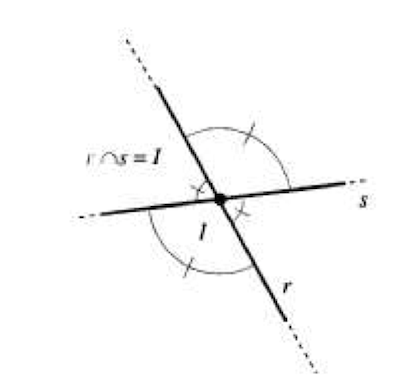
- Se le rette r ed s hanno un punto in comune, vengono dette rette incidenti.
- Il punto \( I = r \cap s \) è detto punto di intersezione tra r ed s.
Rette ortogonali o normali
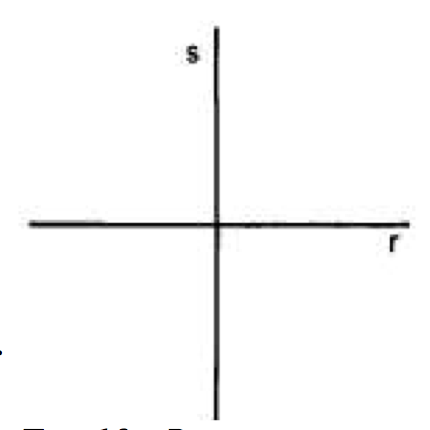
- Due rette incidenti si dicono perpendicolari (o ortogonali, o normali) se, intersecandosi, dividono il piano in quattro angoli uguali.
- Osserviamo che ciascuno di tali angoli sarà 1⁄4 dell'angolo giro, e quindi sarà un angolo retto.
- Per indicare che le rette r ed s sono perpendicolari, si scrive: \(r \perp s \)
Geometria euclidea
- La geometria euclidea è la geometria che si basa sui cinque postulati di Euclide e in particolar modo sul postulato delle parallele.
- Le geometrie che si basano su postulati diversi da quelli elencati da Euclide sono dette geometrie non euclidee.
Postulati di Euclide
- Tra due punti qualsiasi è possibile tracciare una ed una sola retta;
- Si può prolungare un segmento oltre i due punti indefinitamente;
Dato un punto e una lunghezza, è possibile descrivere un cerchio;Tutti gli angoli retti sono congruenti tra loro;
Postulato delle parallele o quinto postulato di Euclide
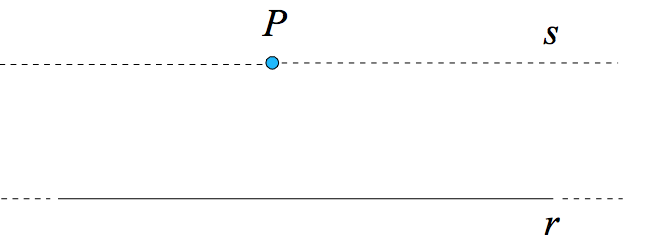
- Data una retta r, e dato un punto P non appartenente ad r, esiste una ed una sola retta s passante per P e parallela ad r.
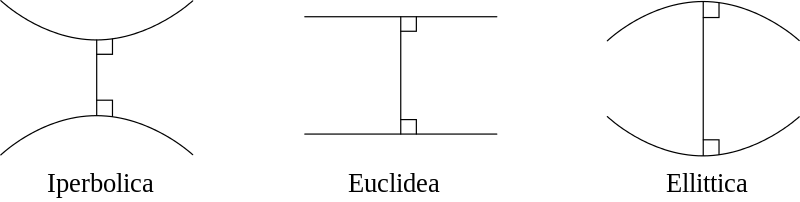
Geometrie alternative
- accettando il postulato delle parallele come l'abbiamo enunciato si ottene la geometria euclidea.
- Possiamo rifiutare il postulato precedente e ammettere che:
- Data una retta r, e dato un punto P non appartenente ad r, non esiste nessuna retta s passante per P e parallela ad r (geometria non euclidea detta di Riemann. )
- Data una retta r, e dato un punto P non appartenente ad r, esistono infinite rette s passanti per P e parallele ad r (geometria non euclidea detta di Lobacevskij)
Conclusione
- Concetti primitivi: punti, rette e piani
- Definizioni: segmento, semiretta, semipiano
- Geometria Euclidea (postulati di Euclide)