Trinagolo

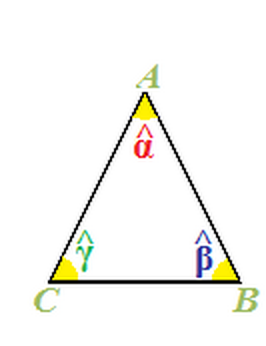
• Il TRIANGOLO è un POLIGONO che ha TRE LATI e TRE ANGOLI
• Un LATO e un ANGOLO del triangolo si dicono OPPOSTI se il VERTICE dell'angolo NON APPARTIENE AL LATO CONSIDERATO
• L'angolo \(\alpha\) è OPPOSTO al lato CB;
• Il lato AB è ADIACENTE agli angoli \(\alpha\) e \(\beta\);

Caratteristiche dei triangoli

• OGNI LATO è sempre MINORE della SOMMA DEGLI ALTRI DUE.
• OGNI LATO è sempre MAGGIORE della DIFFERENZA DEGLI ALTRI DUE.
• La SOMMA degli ANGOLI INTERNI del TRIANGOLO misura 180°

Classificazione dei triangoli 1/2

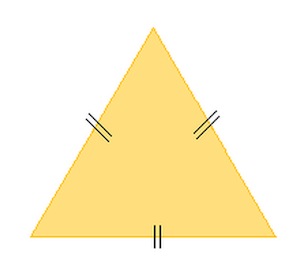
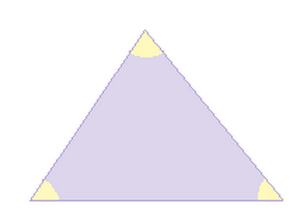
• Il triangolo con tutti e TRE LATI CONGRUENTI, cioè aventi la stessa lunghezza, si dice EQUILATERO. (Ampiezza di un angolo del triangolo equilatero = 180° : 3 = 60°)
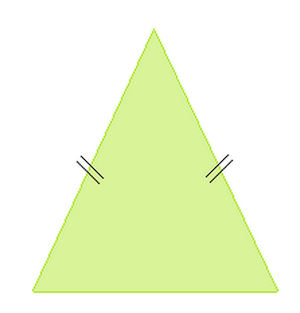
• Il triangolo con DUE LATI CONGRUENTI, cioè aventi la stessa lunghezza, si dice ISOSCELE.
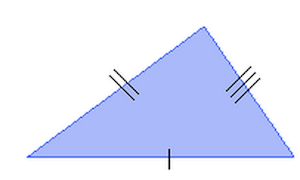
• Il triangolo che ha TRE LATI DISUGUALI, cioè aventi tutti diversa lunghezza, si dice SCALENO.

Classificazione dei triangoli 2/2

• Secondo gli ANGOLI i TRIANGOLI possono essere classificati in:
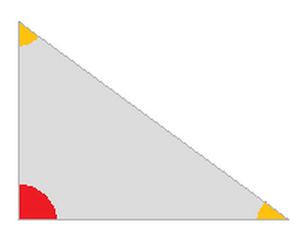
  • Il triangolo che ha un ANGOLO RETTO si dice TRIANGOLO RETTANGOLO.
  • Il triangolo con tutti e TRE gli ANGOLI ACUTI si dice TRIANGOLO ACUTANGOLO.
  • Il triangolo che ha un ANGOLO OTTUSO si dice TRIANGOLO OTTUSANGOLO.

Elementi notevoli di un triangolo

• Gli ELEMENTI NOTEVOLI di un triangolo sono:
• Altezze (Ortocentro)
• Mediane (Baricentro)
• Bisettrici (Incentro)
• Assi (Circocentro)

Altezze di un triangolo

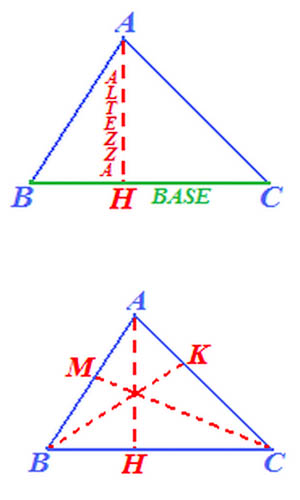
• Disegniamo il segmento AH che parte dal vertice A e interseca, perpendicolarmente, il lato opposto BC
• Il segmento AH si dice ALTEZZA del triangolo relativa al lato BC.
• Il punto H si chiama PIEDE dell'ALTEZZA.
• Mentre il lato BC è la BASE del triangolo.
• l'ALTEZZA di un triangolo rispetto ad un suo lato, che in questo caso prende il nome di BASE, è la DISTANZA di questo LATO dal VERTICE OPPOSTO.
• Poiché il triangolo ha TRE LATI, ognuno di essi può essere considerato come BASE del triangolo.

Mediana

• Disegniamo un qualsiasi triangolo ABC.
• Chimaiamo P il PUNTO MEDIO del lato BC.
• Congiungiamo il vertice A con il punto medio P del lato opposto.
• Quella che abbiamo disegnato prende il nome di MEDIANA e più esattamente essa è la MEDIANA del triangolo ABC relativa al lato BC.
• La MEDIANA di un triangolo è il SEGMENTO che UNISCE un VERTICE al PUNTO MEDIO DEL LATO OPPOSTO.

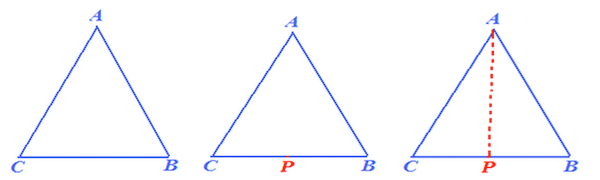
Bisettrice del vertice di un triangolo

• Disegniamo il triangolo ABC
• Disegniamo un segmento che partendo dell'angolo A raggiunga il lato opposto BC, dividendo l'angolo A in due parti aventi la stessa ampiezza
• Il segmento AH disegnato prende il nome di BISETTRICE di VERTICE A del triangolo.

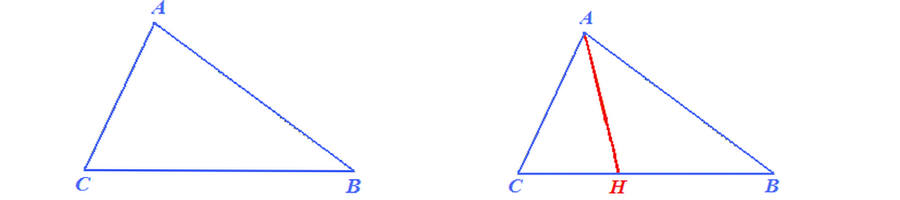
ASSI dei LATI di un TRIANGOLO

• Disegniamo un qualsiasi triangolo ABC
• Ora disegniamo il punto medio del lato BC e lo chiamiamo P
• Ora disegniamo la RETTA p (minuscolo) PERPENDICOLARE a BC e PASSANTE per il PUNTO P
• La RETTA p disegnata si chiama ASSE del LATO BC.
• L'ASSE di un TRIANGOLO relativo ad un lato è la RETTA ad ESSO PERPENDICOLARE passante per il PUNTO MEDIO del lato considerato.

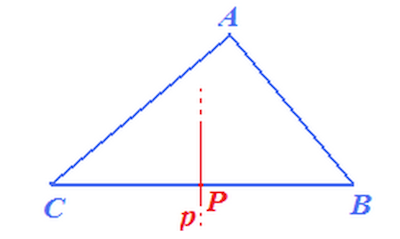
Punti notevoli di un triangolo

• I PUNTI NOTEVOLI di un triangolo sono:
  • l'ORTOCENTRO;
  • il BARICENTRO;
  • l'INCENTRO;
  • il CIRCOCENTRO.

Ortocentro di un triangolo

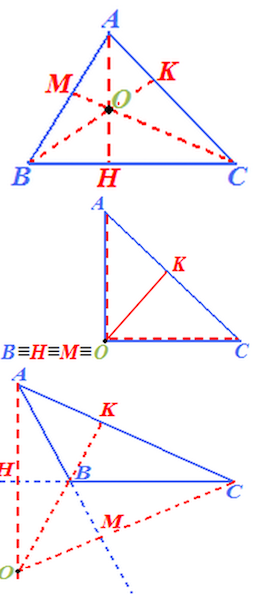
• l'ORTOCENTRO è il PUNTO in cui si INCONTRANO le ALTEZZE di un triangolo.
• Se il triangolo è ACUTANGOLO l'ORTOCENTRO è INTERNO al triangolo
• Se il TRIANGOLO è RETTANGOLO l'ORTOCENTRO COINCIDE con il VERTICE DELL'ANGOLO RETTO.
• Se il TRIANGOLO è OTTUSANGOLO l'ORTOCENTRO è ESTERNO al triangolo.

Baricentro di un triangolo

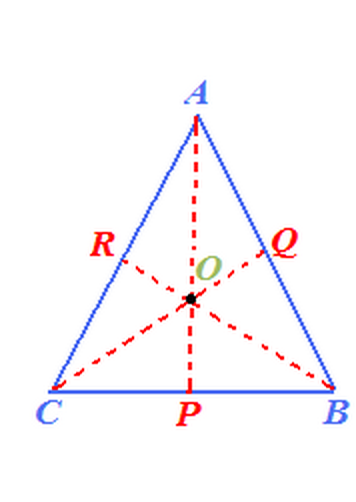
• Poiché il triangolo ha tre lati e tre angoli, possiamo costruire tre mediane per ogni triangolo.
• Ognuna di esse unisce un vertice con il punto medio del lato opposto.
• Le tre mediane passano tutte per uno stesso punto detto BARICENTRO che nell'immagine è indicato con la lettera O.
• La parola BARICENTRO significa "centro del peso", in altre parole esso è l'unico punto di equilibrio di un triangolo.

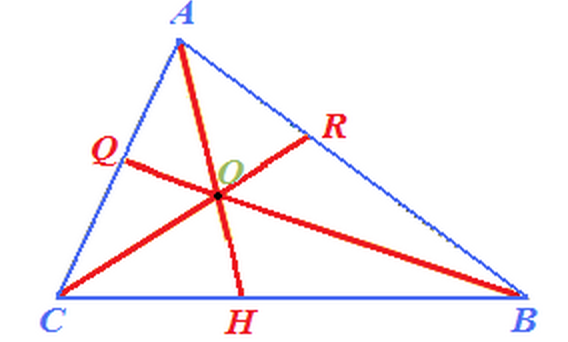
Incentro

• Disegniamo le bisettrici dei triangoli relativi ai vertici A, B e C
• Le TRE BISETTRICI si INCONTRANO in un punto detto INCENTRO che nel disegno è evidenziato con la lettera O
• Per qualsiasi triangolo l'INCENTRO è INTERNO al triangolo.

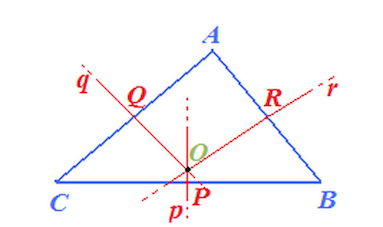
Circocentro del triangolo

• disegniamo il punto medio del lato AB (R) e il punto medio del lato AC (Q)
• disegniamo, rispettivamente, la retta perpendicolare ad AB passante per R che chiamiamo r e la retta perpendicolare ad AC passante per Q che chiamiamo q
• Gli assi del triangolo passano tutti per UNO STESSO PUNTO chiamiamato CIRCOCENTRO DEL TRIANGOLO e che è indicato con la lettera O

Primo teorema di Euclide

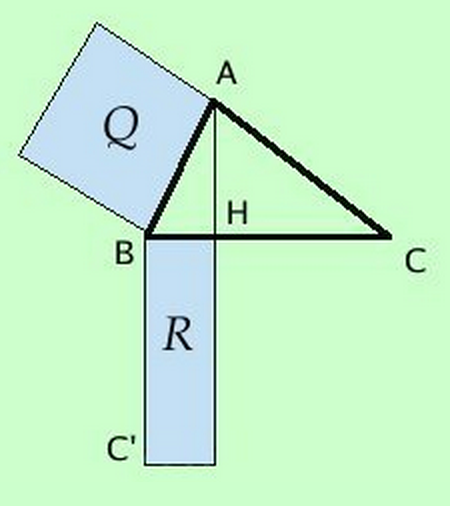
• In ogni triangolo rettangolo il quadrato costruito su un cateto è equivalente ad un rettangolo avente per lati l'ipotenusa e la proiezione del cateto sull'ipotenusa. \[ \overline{AB}^{2} = \overline{BH} * \overline{BC} \]

Teorema di Pitagora

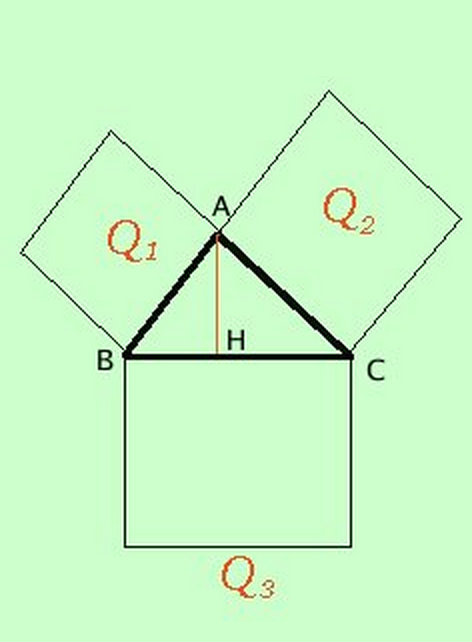
• In ogni triangolo rettangolo la somma dei quadrati costruiti sui cateti è equivalente al quadrato costruito sull'ipotenusa \[ \overline{AB}^{2} + \overline{AC}^{2} = \overline{BC}^{2} \]

Secondo teorema di Euclide

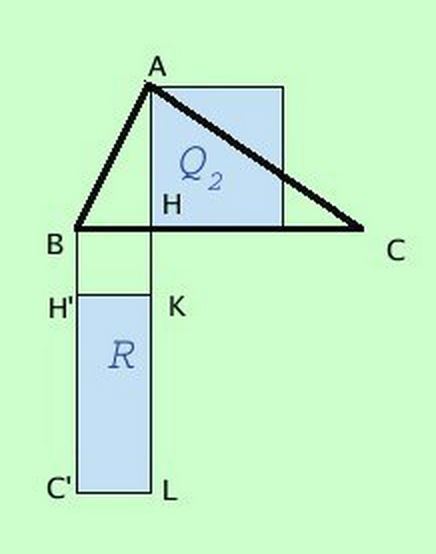
• In ogni triangolo rettangolo il quadrato costruito sull'altezza relativa all'ipotenusa è equivalente al rettangolo che ha per lati le proiezioni dei cateti sull'ipotenusa. \[ \overline{AH}^{2} = \overline{BH} * \overline{HC} \]

Triangolo rettangolo e trigonometria 1/2

• In un triangolo rettangolo, la misura di un cateto è uguale al prodotto della misura dell’ipotenusa per il seno dell’angolo opposto oppure per il coseno dell’angolo adiacente. \[ b = a * \sin{\beta}, c = a * \sin{\gamma} \\ b = a * \cos{\gamma}, c = a * \cos{\beta} \]

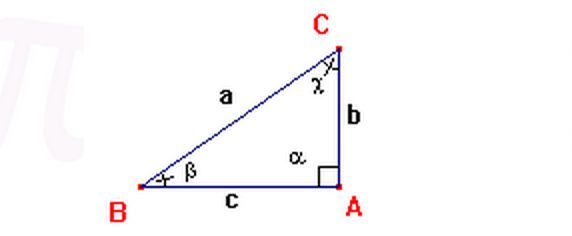
Triangolo rettangolo e trigonometria 2/2

• In un triangolo rettangolo, la misura di un cateto è uguale a quella dell’altro cateto per la tangente dell’angolo opposto al primo, o per la cotangente dell'angolo adiacente. \[ c = b * \tan{\gamma}, b = c * \tan{\beta} \\ c = b * \cot{\beta}, b = c * \cot{\gamma} \]